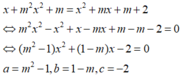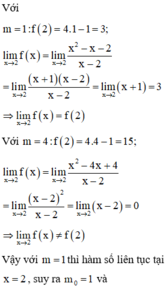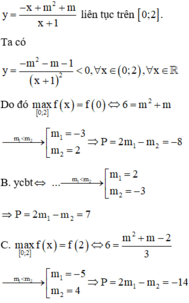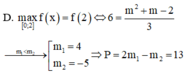Tính M(x) + N(x) biết: M(x) = x2 - mx + m2 ; N(x)= (m+1) x2 + 3mx + m2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 2 2022
a: \(\Leftrightarrow\left(2m+4\right)^2-4m\cdot9=0\)
\(\Leftrightarrow4m^2+16m+16-36m=0\)
\(\Leftrightarrow m^2-5m+4=0\)
\(\Leftrightarrow\left(m-1\right)\left(m-4\right)=0\)
hay \(m\in\left\{1;4\right\}\)
b: \(\Leftrightarrow\left(2m-8\right)^2-4\left(m^2+m+3\right)=0\)
\(\Leftrightarrow4m^2-32m+64-4m^2-4m-12=0\)
=>-36m+52=0
=>-36m=-52
hay m=13/9
d: \(\Leftrightarrow m^2-4m\left(m+3\right)=0\)
\(\Leftrightarrow m\left(m-4m-12\right)=0\)
=>m(-3m-12)=0
=>m=0 hoặc m=-4
6 tháng 2 2022
a) PT có nghiệm kép khi △=0
\(\Leftrightarrow\left[2\left(m+2\right)\right]^2-4.m.9=0\)
\(\Leftrightarrow4\left(m^2+4m+4\right)-36m=0\)
\(\Leftrightarrow4m^2-20m+16=0\Leftrightarrow\left[{}\begin{matrix}m=4\\m=1\end{matrix}\right.\)
Khi đó nghiệm kép của pt là \(x_1=x_2=\dfrac{-2\left(m+2\right)}{2.m}=\dfrac{-2m-4}{2m}=-1-\dfrac{2}{m}\)
+Khi m=4 thì \(x_1=x_2=-1-\dfrac{2}{4}=-\dfrac{3}{2}\)
+Khi m=1 thì \(x_1=x_2=-1-\dfrac{2}{1}=-3\)
AH
Akai Haruma
Giáo viên
2 tháng 12 2023
Lời giải:
a. $y=mx-x^2-2x+mx^2+m=x^2(m-1)+x(m-2)+m$
Lấy $x_1,x_2\in R$ sao cho $x_1\neq x_2$
$y(x_1)=x_1^2(m-1)+x_1(m-2)+m$
$y(x_2)=x_2^2(m-1)+x_2(m-2)+m$
Để hàm đồng biến thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow \frac{x_1^2(m-1)+x_1(m-2)+m-[x_2^2(m-1)+x_2(m-2)+m]}{x_1-x_2}>0$
$\Leftrightarrow \frac{(m-1)(x_1^2-x_2^2)+(m-2)(x_1-x_2)}{x_1-x_2}>0$
$\Leftrightarrow (m-1)(x_1+x_2)+(m-2)>0$
Với mọi $x_1,x_2\in\mathbb{R}$ thì không có cơ sở để tìm $m$ sao cho hàm đồng biến.
b.
Xét tương tự câu 1, với $x_1\neq x_2\in \mathbb{R}$ thì hàm đồng biến khi:
$(m^2-3m+2)(x_1+x_2)+(m-1)>0$
Với mọi $x_1, x_2\in\mathbb{R}$ thì điều này xảy ra khi:
$m^2-3m+2=0$ và $m-1>0$
$\Leftrightarrow (m-1)(m-2)=0$ và $m-1>0$
$\Leftrightarrow m=2$
20 tháng 9 2021
a: Mệnh đề sai
Vd: x=1 thì \(x^2=1< 4\)
b: Mệnh đề đúng
c: Mệnh đề đúng
d: Mệnh đề sai
Vì \(x^2>4\) thì hoặc là x>2 hoặc cũng có thể là x<-2
CM
19 tháng 12 2018
a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 
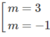
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.
18 tháng 2 2020
a) Số giá trị nguyê của tham số m thuộc (-5;5) để phương trình x2+2mx + m2 +m -3=0 có hai nghiệm phân biệt
