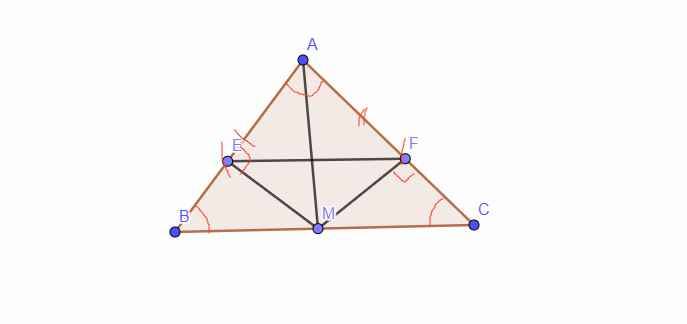
∆ cân ABC (AB = AC). Từ trung điểm M của BC vẽ ME vuông góc AC; MF vuông góc AC. Chứng minh rằng
a) ∆BEM = ∆CFM
b) AE = AF
c) AM là phân giác của góc EMF
d) So sánh MC và ME
Help me :(
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 8 2023
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc AMB=góc AMC=90 độ
=>AM vuông góc BC
b: Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
góc B=góc C
=>ΔBEM=ΔCFM
=>ME=MF
6 tháng 2 2022
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
Xét ΔABC có AE/AB=AF/AC
nên FE//BC
30 tháng 10 2023
Ta có; ΔABC vuông cân tại C
mà CD là đường trung tuyến
nên CD\(\perp\)AB và CD là phân giác của \(\widehat{ACB}\)
=>\(\widehat{ACD}=\widehat{BCD}=\dfrac{90^0}{2}=45^0\)
Gọi O là giao điểm của CM với FE
Xét tứ giác CEMF có
\(\widehat{CEM}=\widehat{CFM}=\widehat{FCE}=90^0\)
=>CEMF là hình chữ nhật
=>CM cắt EF tại trung điểm của mỗi đường và CM=EF
=>O là trung điểm chung của CM và EF và CM=EF
=>OM=OC=OE=OF
=>O là tâm đường tròn ngoại tiếp tứ giác CFME
\(\widehat{CEM}=\widehat{CFM}=\widehat{CDM}=90^0\)
Do đó: C,E,M,F,D cùng thuộc đường tròn đường kính CM
=>C,E,M,F,D cùng thuộc (O)
=>D thuộc (O)
Xét (O) có
ΔDFE nội tiếp
FE là đường kính
Do đó: ΔDFE vuông tại D
Xét tứ giác FDEC có
\(\widehat{FCE}+\widehat{FDE}=180^0\)
=>FDEC là tứ giác nội tiếp
=>\(\widehat{DFE}=\widehat{DCE}=\widehat{DCA}=45^0\)
Xét ΔDFE vuông tại D có \(\widehat{DFE}=45^0\)
nên ΔDFE vuông cân tại D
14 tháng 4 2023
a: Xet ΔBME vuông tại M và ΔBAC vuông tại A có
góc B chung
=>ΔBME đồng dạng với ΔBAC
b: Xét ΔMBE vuông tại M và ΔMNC vuông tại M có
góc MBE=góc MNC
=>ΔMBE đồng dạng với ΔMNC
=>MB/MN=ME/MC
=>MN*ME=MB*MC=1/4BC^2
=>BC^2=4*MN*ME
14 tháng 4 2023
a) xét △ABC và △MBE có :
Góc BAC = Góc BME = 90 (Gt)
Góc B chung
⇒△ABC ∼ △MBE (g.g) (1)
b)Xét △ABC và △MCN có:
Góc BAC = góc NMC = 90 (Gt)
⇒△ABC ∼ △MBE (g.g) (2)
Ta có M là tđ của BC ⇒ MB =MC =1/2 BC
Từ (1) và (2) ⇒△MNC ∼ △MBE
⇒EM/MC = MN/BM
⇔ EM/MN = 1/2BC : 1/2BC
⇔BC2 =EM/MN : 4
⇔BC2 = EM/4MN
16 tháng 3 2022
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Ta có: ΔBAC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó; ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M
c: BC=6cm nên BM=CM=3cm
=>AM=4cm
d: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
9 tháng 1 2023
a, Vì Tam giác `ABC` cân tại A `=> AB = AC ;`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM chung`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `AMC (c-g-c)`
b, Vì Tam giác `AMB =` Tam giác `AMC (a)`
`=>` \(\widehat{EAM}=\widehat{FAM}\) (2 góc tương ứng).
Xét Tam giác `EAM` và Tam giác `FAM` có:
AM chung
\(\widehat{EAM}=\widehat{FAM}\) `(CMT)`
\(\widehat{AEM}=\widehat{AFM}=90^0\)
`=>` Tam giác `EAM =` Tam giác `FAM (ch-gn)`
`=> EA = FA` (2 cạnh tương ứng).
c, *câu này mình hơi bí bn ạ:')
9 tháng 1 2023
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
Ta có hình sau :
Chứng minh :
a) Vì △ABC cân ( AB = AC ) ⇒ △ABC cân tại A
⇒ \(\widehat{ABC}=\widehat{ACB}\left(\text{t/c t/g cân}\right)\)
Xét △BEM vuông tại E và △CFM vuông tại F có :
BM = MC ( gt )
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
⇒ △BEM = △CFM ( cạnh huyền - góc nhọn )
⇒ EM = FM ( tương ứng )
b)Nối A với M
Xét △AME vuông tại E và △AMF vuông tại F có:
AM - cạnh chung
EM = FM ( cmt )
⇒ △AME = △AMF (cạnh huyền - cạnh góc vuông )
⇒ AE = AF ( tương ứng )
c) Có △AME = △AMF ( cmt )
⇒ \(\widehat{AME}=\widehat{AMF}\) ( tương ứng )
⇒ AM là tia phân giác của \(\widehat{EMF}\)
Còn câu d đâu bạn