Bài 7. (3 điểm) Cho hai đường tròn (O;R) và (O';r) tiếp xúc ngoài tại A. Tiếp tuyến chung ngoài MN cắt tiếp tuyến chung trong tại K (M, N là 2 tiếp điểm; M ∈ (O) và N ∈ (O')). a) Chứng minh AK = MK và △AMN là tam giác vuông. b) MA cắt (O') tại B, NA cắt (O) tại C. Chứng minh SAMN = SABC. c) Chứng minh BK và ON cắt nhau tại một điểm nằm trên (O').
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD

a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
Xét ΔBAM vuông tại B có BD là đường cao
nên \(AD\cdot AM=AB^2=4R^2\)

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC

Bài 7:
a: Xét ΔOAM vuông tại A có
\(\cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AOM}=60^0\)
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=180^0\)
Do đó: OAMB là tứ giác nội tiếp
Suy ra: \(\widehat{AOB}=180^0-36^0=144^0\)

b: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
=>BHCD là hình bình hành
=>BH//CD và BD//CH
ta có: BH//CD
BH\(\perp\)AC
Do đó: CD\(\perp\)CA
=>ΔCDA vuông tại C
=>ΔCAD nội tiếp đường tròn đường kính AD(1)
Ta có: BD//CH
CH\(\perp\)AB
Do đó: BD\(\perp\)BA
=>ΔBAD vuông tại B
=>ΔBAD nội tiếp đường tròn đường kính AD(2)
Từ (1) và (2) suy ra B,A,D,C cùng thuộc (O), đường kính AD
Xét (O) có
ΔAID nội tiếp
AD là đường kính
Do đó: ΔAID vuông tại I
=>AI\(\perp\)ID tại I
=>AI\(\perp\)IH tại I
=>ΔAIH vuông tại I
=>I nằm trên đường tròn đường kính AH(3)
ta có: \(\widehat{AFH}=\widehat{AEH}=90^0\)
=>A,F,H,E cùng thuộc đường tròn đường kính AH(4)
Từ (3) và (4) suy ra A,F,I,H,E cùng thuộc một đường tròn

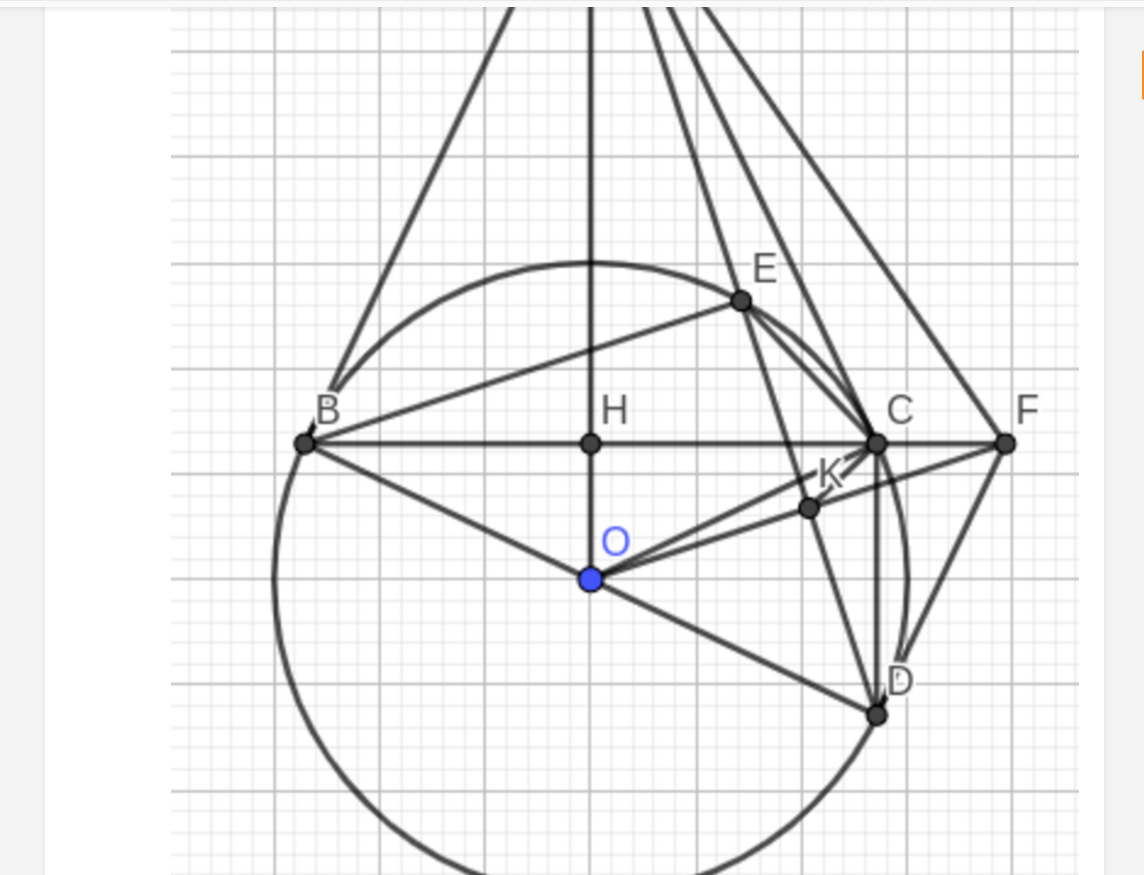
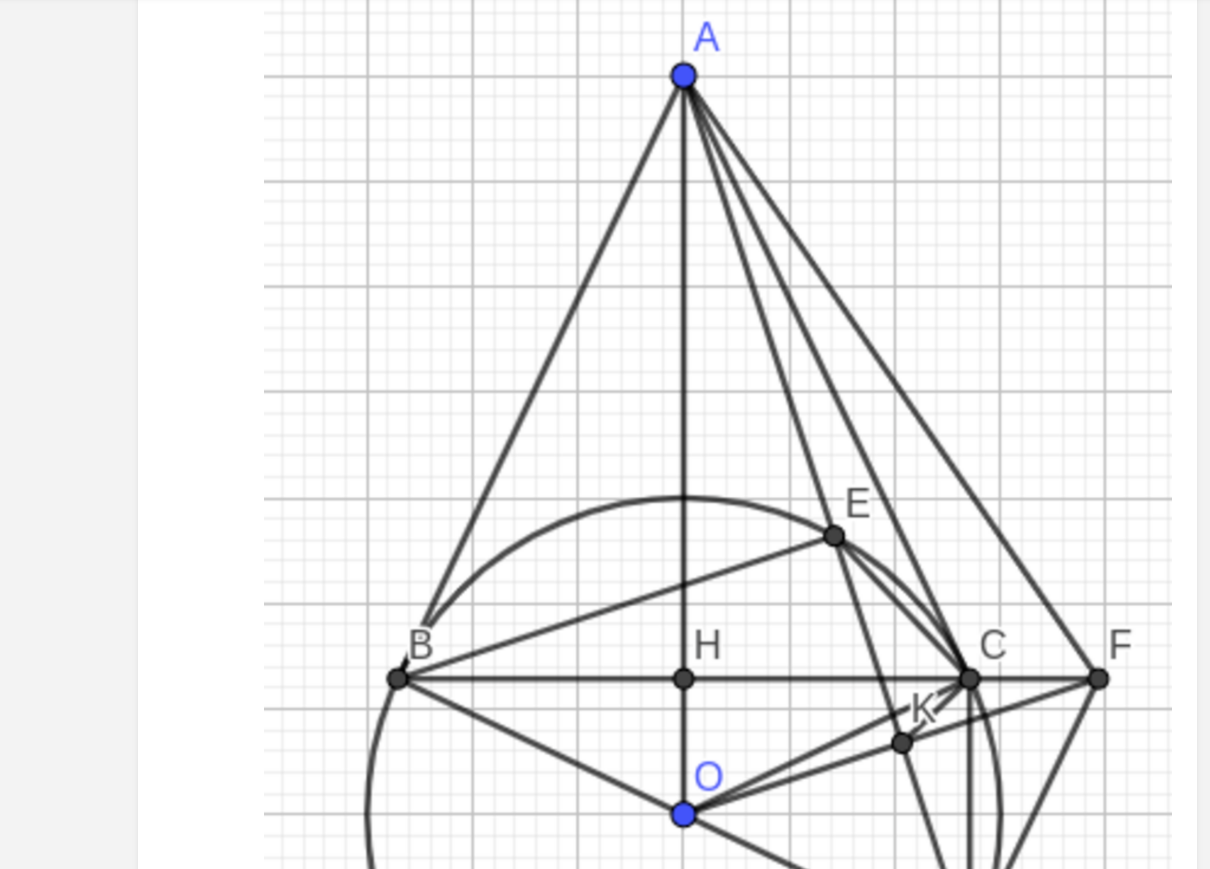
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp(1)
Xét tứ giác OKAB có
\(\widehat{OKA}+\widehat{OBA}=180^0\)
Do đó: OKAB là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra A,B,O,K,C cùng nằm trên đường tròn


a: Xét (O) có
KM,KA là các tiếp tuyến
Do đó: KM=KA(1)
Xét (O') có
KA,KN là các tiếp tuyến
Do đó: KA=KN(2)
Từ (1) và (2) suy ra KM=KN
mà M,K,N thẳng hàng
nên K là trung điểm của MN
Xét ΔAMN có
AK là đường trung tuyến
\(AK=\dfrac{MN}{2}\left(=MK\right)\)
Do đó: ΔAMN vuông tại A