Cho tam giác ABC cân đỉnh A, đường cao AI; M, N lần lượt là trung điểm của AB, ÁC. Viết tất cả các cặp đoạn thẳng = nhau có thể, các cặp góc = nhau có thể. Giải thích tại sao = nhau, có góc nào trong hình = 90 độ ko.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 5 2019
+) Xét tam giác vuông BKM có ∠BMC là góc ngoài tam giác tại đỉnh M nên:
CM
24 tháng 10 2017
Do Tam giác ABC cân tại A, AH là đường cao nên H là trung điểm BC.
+Đáp án A. Ta có
18 tháng 5 2022
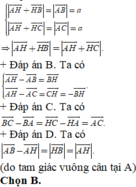
Gọi giao điểm của BM với AC; CM với AD lần lượt là D và E
Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó;ΔEBC=ΔDCB
Suy ra: \(\widehat{MCB}=\widehat{MBC}\)
hay ΔMBC cân tại M
=>\(\widehat{MBC}=\dfrac{180^0-140^0}{2}=20^0\)
=>\(\widehat{ACB}=\widehat{ABC}=70^0\)
hay \(\widehat{BAC}=40^0\)
HT
9 tháng 4 2017
HÌNH BẠN TỰ KẺ NHÉ!!!!!!!!
kẻ NE vuông gócAM, DI vuông góc AM
Có: góc DAI = góc ABH (cùng phụ vs BAH)
Xét tam giác BAH = tam giác ADI (ch.gn) => AH = DI (2 cạnh t/ứ) (1)
Có: góc MAE = góc HCA (cùng phụ vs HAC)
Xét tam giác AHC = tam giác ENA (ch>gn)=> AH = NE (2 cạnh t/ứ) (2)
Từ (1) và (2) => DI = NE
Xét tam giác DMI = tam giác EMN (g.c.g) (tự cm góc MDI = góc NEM)
=> DM = ME (đpcm)
19 tháng 9 2023
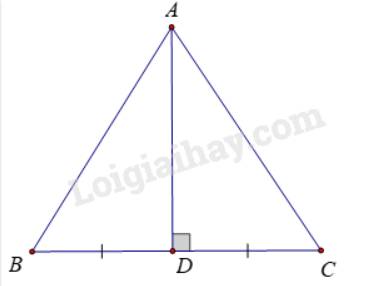
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)
\( \Rightarrow AD\)là đường trung trực của BC.
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)
\( \Rightarrow \)AD là tia phân giác góc BAC.
Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
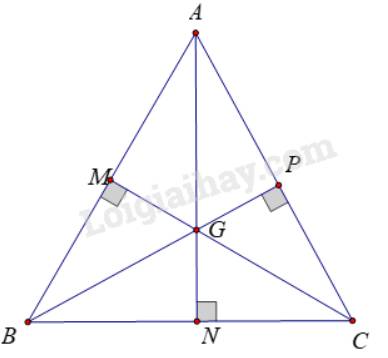
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC
\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất
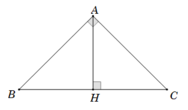
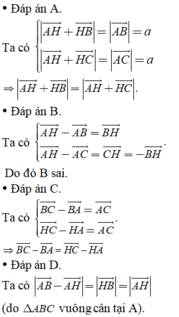
2 TG IBA = tg ICA(c-g-c)
2 TG IMA=TG INA(c-g-c) (1)
Các cặp cạnh bằng nhau:
AM=BM vì M là trung điểm của AB
AN=CN vì N là trung điểm của AB
AB=AC vì Tam giác ABC cân.
MI=NI vì (1)
Các góc bằng nhau:
AIB = AIC do AI là đường cao của tam giác ABC.
CBA = BCA vì tam giác ABC cân
IAB=IAC vì tg IBA=ICA
IMA=INA vì (2)
IMB=INC vì góc IMA=INA,mà 2 góc IMB kề bù IMA,INC kề bù INA.
Các góc bằng 90*: BIA và CIA