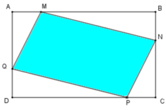
Cho hình bình hành ABCD. Ta kẻ đường thẳng ∆ nằm ngoài hình bình hành. Hạ AM, BN, CP, DQ vuông góc ∆; M, N, P, Q ∈ ∆. Chứng minh rằng 𝐴𝑀 + 𝐶𝑃 = 𝐵𝑁 + 𝐷𝑄
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 7 2023
Xét ΔMBN và ΔPDQ có
MB=PD
góc B=góc D
BN=DQ
=>ΔMBN=ΔPDQ
=>MN=PQ
Xét ΔAMQ và ΔCPN có
AM=CP
góc A=góc C
AQ=CN
=>ΔAMQ=ΔCPN
=>MQ=PN
mà MN=PQ
nên MNPQ là hình bình hành
CM
6 tháng 10 2019
Theo đề bài ta có:
AM = CP = 35 : 5 = 7cm
BN = DQ = 18 : 3 = 6cm
Từ đó ta có:
BM = DP = 35 – 7 = 28cm
AQ = CN = 18 − 6 = 12cm
Diện tích tam giác AMQ là :
7 × 12 : 2 = 42 ( c m 2 )
Diện tích tam giác BMN là :
28 × 6 : 2 = 84 ( c m 2 )
Diện tích tam giác CPN là :
7 × 12 : 2 = 42 ( c m 2 )
Diện tích tam giác DPQ là :
28 × 6 : 2 = 84 ( c m 2 )
Diện tích hình chữ nhật ABCD là :
35 × 18 = 630 ( c m 2 )
Diện tích hình bình hành MNPQ là:
630 − (42 + 84 + 42 + 84) = 378 ( c m 2 )
Đáp số: 378 .
Vậy đáp án đúng điền vào ô trống là 378.
27 tháng 1 2021
Ta có: AM = CP = 1/4AB => AM = CP = 1/4 x 28 = 7 (cm) => BM = DP = 28 - 7 = 21 (cm)
BN = DQ = 1/3BC = 1/3 x 18 = 6 (cm) => AQ = NC = 18 - 6 = 12 (cm)
St/giác AMQ = 1/2 xAM x AQ = 1/ 2 x 7 x 12 = 42 (cm2)
St/giác MBN = 1/2 x MB x BN = 21 x 6 x 1/2 = 63 (cm2)
St/giác NPC = 1/2 x NC x CP = 1/2 x 12 x 7 = 42 (cm2)
St/giác QDP = 1/2 x QP x DP = 1/2 x 21 x 6 = 63 (cm2)
SHCN ABCD = 28 x 18 = 504 (cm2) => Shình bình hành MNPQ = 504 - (2 x 42 + 63x 2) = 294 (cm2)
25 tháng 11 2019
a)
Vì BN = DQ , AD = BC => AD - DQ = BC - BN hay AQ = NC
Xét tam giác AQM và CNP có:
\(\hept{\begin{cases}AQ=CN\\AM=CP\\\widehat{QAM}=\widehat{NCP}\left(doABCDl\text{à}hbh\right)\end{cases}}\)
\(\Rightarrow\Delta AQM=\Delta CNP\left(c.g.c\right)\Rightarrow QM=NP\)
Hoàn toàn tương tự: △MBN=△PDQ(c.g.c)⇒MN=PQ
Tứ giác MNPQMNPQ có 2 cặp cạnh đối bằng nhau nên là hình bình hành.
=> MNPQ là hình bình hành.
b) Gọi K là giao điểm của AC và MP
Xét tam giác AKM và CKP ta có:
\(\hept{\begin{cases}\widehat{KAM}=\widehat{KCP}\left(slt\right)\\\widehat{KMA}=\widehat{KPC\left(slt\right)}\\\Rightarrow AM=CP\end{cases}}\)
\(\Rightarrow\Delta AKM=\Delta CKP\left(g.c.g\right)\)
\(\Rightarrow AK=CK;KM=KP\left(1\right)\)
Vì ABCDABCD là hình bình hành nên hai đường chéo AC,BDAC,BD cắt nhau tại trung điểm mỗi đường. Tương tự, MNPQMNPQ là hình bình hành nên MP,QNMP,QN cắt nhau tại trung điểm mỗi đường
Mà từ (1)(1) suy ra KK là trung điểm của AC,MPAC,MP, do đó KK cũng là trung điểm của BD,QNBD,QN
Do đó AC,BD,MP,NQAC,BD,MP,NQ đồng quy tại (trung điểm) KK.
19 tháng 4 2021
Diện tích hình bình hành MNPQ bằng diện tích hình chữ nhật ABCD trừ đi tổng diện tích
của bốn hình tam giác MAQ, MBN, PCN và QDP.
Ta có:
AM = GP = 28 : 4 = 7 (cm) ;
BN = DQ = 18 : 3 = 6 (cm) ;
MB = 28 – 7 = 21 (cm) ;
AQ = 18 – 6 = 12 (cm).
Diện tích hình tam giác MAQ ( hoặc tam giác PCN ) là :
7 x 12 : 2 = 42 (cm2)
Diện tích hình tam giác MBN ( hoặc tam giác QDP ) là :
21 x 16 : 2 = 63 (cm2)
Diện tích hình chữ nhật ABCD là :
28 x 18 = 504 (cm2)
Diện tích hình bình hành MNPQ là :
504 – ( 42x 2 + 63 x 2 ) = 294 (cm2