Cho tam giác ABC vuông tại B; K là trung điểm của AC . Trên tia đối của KB lấy D sao cho KD = KB.
a. Chứng minh: tam giác ABK = CKD
b. Gọi H là trung điểm của BC; AH cắt BD tại M; DH cắt AC tại N. C/m rằng góc MHB=NHC
c. C/m: Tam giác HMN cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 2 2021
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=BC^2+AB^2\)
\(\Leftrightarrow AB^2=AC^2-BC^2=12^2-8^2=80\)
hay \(AB=4\sqrt{5}cm\)
Vậy: \(AB=4\sqrt{5}cm\)
Bài 2:
Áp dụng định lí Pytago vào ΔMNP vuông tại N, ta được:
\(MP^2=MN^2+NP^2\)
\(\Leftrightarrow MN^2=MP^2-NP^2=\left(\sqrt{30}\right)^2-\left(\sqrt{14}\right)^2=16\)
hay MN=4cm
Vậy: MN=4cm
9 tháng 2 2021
Bài 1 :
- Áp dụng định lý pi ta go ta được :\(BA^2+BC^2=AC^2\)
\(\Leftrightarrow AB^2+8^2=12^2\)
\(\Leftrightarrow AB=4\sqrt{5}\) ( cm )
Vậy ...
Bài 2 :
- Áp dụng định lý pi ta go vào tam giác MNP vuông tại N có :
\(MN^2+NP^2=MP^2\)
\(\Leftrightarrow MN^2+\sqrt{14}^2=\sqrt{30}^2\)
\(\Leftrightarrow MN=4\) ( đvđd )
Vậy ...
7 tháng 3 2022
a: Xét ΔABC vuông tại B và ΔAED vuông tại E có
AC=AD
\(\widehat{A}\) chung
Do đó: ΔABC=ΔAED
b: Đề sai rồi bạn
17 tháng 8 2023
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
CM
29 tháng 4 2018
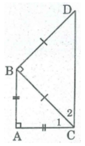
Vì ΔABC vuông cân tại A nên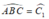 
Lại có: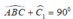 
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên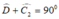 
Lại có: 
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.
2 tháng 9 2023
ΔBDC vuông cân tại B
=>góc BCD=góc BDC=45 độ
ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc ABC=góc DCB
mà hai góc này ở vị trí so le trong
nên AB//DC
mà AB vuông góc AC
nên DC vuông góc AC
Xét tứ giác ABDC có
AB//DC
góc CAB=90 độ
Do đó: ABDC là hình thang vuông
30 tháng 6 2023
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: Xét ΔEBC có góc EBC=góc ECB
nên ΔEBC cân tại E
mà EH là đường cao
nên H là trung điểm của BC
=>HB=HC
d: Xét ΔEAI vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEI=góc HEC
=>ΔEAI=ΔEHC
=>EI=EC>EH
B
11 tháng 1 2023
+)ΔABC vuông tại A \(\Rightarrow\widehat{A}=90^o\)
+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC, ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(=>90^o+40^o+\widehat{C}=180^o\)
\(=>\widehat{C}=180^o-90^o-40^o=50^o\)
Vậy \(\widehat{C}=50^o\)
------------------------------------------
+)Tam giác ABC vuông tại B \(\Rightarrow\widehat{B}=90^o\)
+)\(\widehat{A}=2.\widehat{C}\Rightarrow\widehat{A}+\widehat{C}=2.\widehat{C}+\widehat{C}=3.\widehat{C}\)
+)Áp dụng định lý tổng ba góc trong tam giác vào tam giác ABC, ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{A}+90^o+\widehat{C}=180^o\)
\(=>\widehat{A}+\widehat{C}=180^o-90^o\)
\(=>3.\widehat{C}=90^o\)
\(=>\widehat{C}=\dfrac{90^o}{3}=30^o\)
+)\(\widehat{A}=2.\widehat{C}\Rightarrow\widehat{A}=2.30^o=60^o\)
Vậy: \(\widehat{A}=60^o\) ; \(\widehat{C}=30^o\)
11 tháng 1 2023
1: góc C=90-40=50 độ
2: góc A=2/3*90=60 độ
góc C=90-60=30 độ
a) xét tam giác ABK và CKD có
AK=KC (vì k là trung điểm của AC)
BK=KD (gt)
góc BKA=DKC (đối đỉnh)
=>tam giác ABK=CKD
b) ta có \(\widehat{ABK}=\widehat{CKD}\)(2 góc tương ứng)
mà 2 góc ở vị trí SLT
nên AB//CD
mà AB=CD (2 cạnh tương ứng)
nên tứ giác ABCD là hình bình hành
+xét \(\Delta ABC\)vuông tại B có đường trung tuyến ứng với cạnh huyền
nên BK=AK=KC
mà BK=KD
=>AK=BK=CK=DK
ta có AK+CK=BK+DK hay BD=AC
xét hình bình hành ABCD có hai đường chéo AC=BD nên ABCD là hình chữ nhật
+xét \(\Delta ABH\)và\(\Delta DCH\)có
BH=CH(gt)
AB=CD(cmt)
\(\widehat{ABH}=\widehat{DCH}=90^o\)(vì ABCD là HCN)
=>\(\Delta ABH=\Delta DCH\)=>\(\widehat{AHB}=\widehat{DHC}\)(2 góc tương ứng)
c)vì BK=CK => tam giác BKC cân
=>góc KBH=KCH
xét \(\Delta BMH\)và\(\Delta CNH\)có
góc KBH=KCH(cmt)
góc AHB=DHC(cmt)
BH=CH (gt)
=>\(\Delta BMH=\Delta CNH\)
=>MH=NH
xét tam giác MHN có
MH=NH=> MHN cân tại H