Cho ABCD là hình chữ nhật (AB>AD). Điểm E thuộc AD ; I,K thuộc CD sao cho DI=CK. Đường thẳng vuông góc vời EK tại K cắt BC tại M.
Tính góc EIM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 12 2021
a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
M
5 tháng 9 2023
a] Để chứng minh AF // BD, ta cần chứng minh tỉ số đồng dạng giữa các cặp cạnh tương ứng của hai tam giác ACF và BDE. Ta có:
AC/BD = AD/BE (vì AF // BD) AC/AD = BE/BD (vì AM // BD và BN // BD)
Từ hai tỉ số trên, ta có:
AC/AD = BE/BD
Vậy, ta đã chứng minh được AF // BD.
b] Để chứng minh E là trung điểm CF, ta cần chứng minh CE = EF và CF // AB. Ta có:
CE = AM (vì CE // AM và AC // BD) EF = BN (vì EF // BN và AC // BD)
Vậy, ta đã chứng minh được E là trung điểm CF.
CM
28 tháng 4 2019
Vì E thuộc cạnh AB nên EB < AB hay 2x < y
Ta có: AE = AB – EB = y – 2x (cm)
AG = AD + DG = y + (3/2) EB = y + (3/2) .2x = y + 3x (cm)
Diện tích hình chữ nhật bằng diện tích hình vuông nên ta có phương trình:
(y – 2x)(y + 3x) = y 2
Theo định lí Pitago, ta có: F C 2 = E B 2 + D G 2
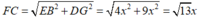
Chu vi ngũ giác ABCFG:
PABCFG = AB + BC + CF + FG + GA
= AB + BC + CF + FG + GD + DA
= y + y + x 13 + y – 2x + 3x + y = x(1 + 13 ) + 4y
Vì chu vi ngũ giác ABCFG bằng 100 + 4 13 (cm) nên ta có phương trình:
x(1 + 13 ) + 4y = 100 + 4 13
Ta có hệ phương trình:
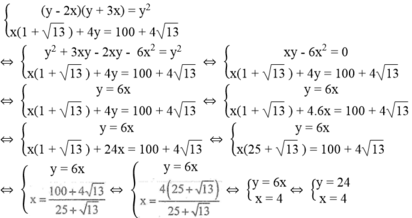
Giá trị của x và y thỏa điều kiện bài toán.
Vậy x = 4 (cm), y = 24 (cm).