Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

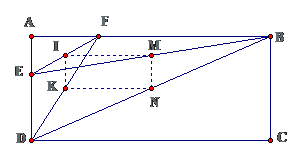
Ta đi chứng minh tứ giác IKMN là hình chữ nhật
+) Theo giả thiết có : là hình bình hành
+) là hình chữ nhật

Xét tam giác FEB ta có
\(\hept{\begin{cases}EI=IF\left(gt\right)\\EM=MB\left(gt\right)\end{cases}}\)
=> IM là đường trung bình của tam giác FEB
IM=1/2FB
\(\hept{\begin{cases}IMsongsongFB\\màAnằmtrenFB\end{cases}}\)
=> IM // AB(1)
Xét tam giác FDB có
\(\hept{\begin{cases}DK=KF\left(gt\right)\\DN=NB\left(gt\right)\end{cases}}\)
=>KN là đường trung bình cảu tam giác FDB
=> KN = 1/2 DB
\(\hept{\begin{cases}IM=\frac{1}{2}FB\left(cmt\right)\\KN=\frac{1}{2FB}\left(cmt\right)\end{cases}}\)
=>IM=KN(2)
Từ (1) và (2) => IMKN là hình bình hành
Xét tam giác EFD có
\(\hept{\begin{cases}EI=IF\left(gt\right)\\DK=KF\left(gt\right)\end{cases}}\)
=> IK là đường trung bình của tam giác EFD
\(\hept{\begin{cases}=>IKsongsongED\\màĂtrenED\end{cases}}\)
\(\hept{\begin{cases}=>IKsongsongDA\\ADvuonggocAB\left(hìnhchunhatABCD\right)\end{cases}}\)
\(\hept{\begin{cases}=>IKvuonggocAB\\IMsongsongAB\left(cmt\right)\end{cases}}\)
=>IM vuông góc IK
=> IKMN là hình chữ nhật
=>IN=KM

ABCDIKEFNM----
a) Vì ABCD là hcn => AB//CD; AB=CD
Mà E,F lần lượt là trung điểm của AB và CF
=> EA=EB=1/2AB;DF=FC=1/2DC và EA//FC
=> EA=FC;EA//FC
Do đó AECF là hbh ( 2 cạnh đối // và = nhau)
b)
Vì ABCD là hcn => AB//CD; AB=CD
Mà E,F lần lượt là trung điểm của AB và CF
=> EA=EB=1/2AB;DF=FC=1/2DC và EA//DF
=> EA=DF;EA//DF
=> AEFD là hbh ( ( 2 cạnh đối // và = nhau)
Lại có: ^ADF=90o ( ABCD là hcn)
Do đó: AEFD là hcn. ( hbh có 1 góc vuông) (đpcm)
c) Vì A đối xứng với N qua D (gt)
=> AN là đường trung trực của ^MAF
=> MA=AF (1)
Vì M đối xứng với F qua D
<=>MF là đường trung trực của ^AMN
=>MA=MN (2)
<=> FM là đường trực của ^AFN
=>AF=NF (3)
Từ (1);(2) và (3) => AM=MN=NF=AF
Nên: AMNF là hình thoi (tứ giác có 4 góc vuông ) (đpcm)
d) ngu câu hình cuối nên bỏ đi để làm n'
mình chứng minh DK đg trung tuyến nw o khả quan lắm :)) nên bỏ
HS chứng minh IMNK là hình chữ nhật Þ IN = KM