Một gen có 57 vòng xoắn và 1490 liên kết hiđrô. Tính theo lí thuyết, số lượng từng loại nuclêôtit của gen là:
A. A = T = 220; G = X = 350.
B. A = T = 250; G = X = 340.
C. A = T = 340; G = X = 250.
D. A = T = 350; G = X = 220.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Áp dụng các công thức:
CT liên hệ giữa chu kỳ xoắn và tổng số nucleotit C=N/20 (Å)
CT tính số liên kết hidro : H=2A +3G
Sô nucleotit môi trường cung cấp cho quá trình nhân đôi n lần: Nmt = N×(2n – 1)

Đáp án A
Phương pháp:
Áp dụng các công thức:
CT liên hệ giữa chu kỳ xoắn và tổng số nucleotit
![]()
CT tính số liên kết hidro : H=2A +3G
Sô nucleotit môi trường cung cấp cho quá trình nhân đôi n lần: Nmt = N×(2n – 1)
Cách giải:
NB = 65 ×20 =1300
HB = 2AB + 3GB = 1669
Ta có hệ phương trình
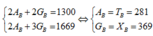
gen Bb nguyên phân bình thường hai lần liên tiếp, môi trường nội bào đã cung cấp 1689 nuclêôtit loại timin và 2211 nuclêôtit loại xitôzin
Tmt = (TB + Tb)(22 – 1) = 1689 → Tb = 282
Xmt = (XB + Xb)(22 – 1) = 2211 → Xb = 368
Hb =1668
Xét các phát biểu :
I đúng
II sai
III đúng
IV đúng

Phương pháp:
Áp dụng các công thức:
CT liên hệ giữa chu kỳ xoắn và tổng số nucleotit C = N 20 (Å)
CT tính số liên kết hidro : H =2A +3G
Số nucleotit môi trường cung cấp cho quá trình nhân đôi n lần: Nmt = N×(2n - 1).
Cách giải:
N B = 65 × 20 = 1300
H B = 2 A B + 3 G B = 1669
Ta có hệ phương trình 2 A B + 2 G B = 1300 2 A B + 3 G B = 1669 ⇔ A B = T B = 281 G B = X B = 369
gen Bb nguyên phân bình thường hai lần liên tiếp, môi trường nội bào đã cung cấp 1689 nuclêôtit loại timin và 2211 nuclêôtit loại xitôzin
T m t = ( T B + T b ) = 1689 → T b = 282
X m t = ( X B + X b ) = 2211 → X b = 368
H
b
=
1668
Xét các phát biểu:
I đúng
II sai
III đúng
IV đúng
Chọn A

\(L = 3,4 . (N/2)\) \(\rightarrow\) \(2040=3,4.(\dfrac{N}{2})\)\(\rightarrow\) \(N=1200(nu)\)
\(\rightarrow\)\(\left\{{}\begin{matrix}A-G=120\\2A+2G=1200\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}A=T=360\left(nu\right)\\G=X=240\left(nu\right)\end{matrix}\right.\)
Ta có \(C= N/20=1200/20=60\) \(\overset{o}{A}\)
\(A=T=360/1200.100\)%\(=30\) %
\(G=X=\)\(\dfrac{240}{1200}.100\%=\)\(20\%\)
\(\text{H = 2A + 3G}\)\(=1440\left(lk\right)\)

Đáp án B
Ta có %A+%G=50% →nucleotit loại khác kia là X, hay %X+%G=60% →%X=%G=30%.
Ta có H=2A+3G= N + G= 130%N → N =2130
→A=T=20% ×2130 = 426 ; G=X=639
Ở mạch 3’ → 5’ (gọi là mạch 1) có A1+T1 = A = T 1 5 + T 1 = 6 5 T 1 =426 → T 1 = 355 = A 2 → A 1 = T 2 = 71
→G1 = 71×3=213 =X2 ; G1 = 639 – 213 =426

Đáp án B
Ta có %A+%G=50% →nucleotit loại khác kia là X, hay %X+%G=60% →%X=%G=30%.
Ta có H=2A+3G= N + G= 130%N → N =2130
→A=T=20% ×2130 = 426 ; G=X=639
Ở mạch 3’ → 5’ (gọi là mạch 1) có A1+T1 = A = ![]()
→G1 = 71×3=213 =X2 ; G1 = 639 – 213 =426
Đáp án A
C = N 20 = 57 →N = 57 × 20 = 1140 →A + G = N 2 = 570
H = 2A + 3G = 1490
Giải hệ phương trình: A + G = 570 2 A + 3 G = 1490