Cho tam giác ABC cân tại A. Vẽ AD vuông góc với BC tại D. a) Chứng minh DB = DC. b) Vẽ DE vuông góc với AB tại E. Đường thẳng song song với AB vẽ từ D cắt AC tại K. Tính EK biết DE = 6cm; DK= 8cm. c) Chứng minh tam giác DKC cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 2 2020
https://lazi.vn/edu/exercise/cho-tam-giac-abc-co-goc-a-120-do-duong-phan-giac-ad-d-thuoc-bc-ve-de-vuong-goc-voi-ab-df-vuong-goc
15 tháng 2 2020
a) ΔAED=ΔAFDΔAED=ΔAFD(ch-gn)nên DE=DF.(hai cạnh tương ứng)
Mặt khác dễ dàng chứng minh được EDFˆ=60o
Vì vậy tam giác DEF là tam giác đều
b)ΔEDK=ΔFDT(hai cạnh góc vuông)
nen DK=DI(hai cạnh tương ứng).Do đó Tam giác DIK cân ở D
c) AD là tia phân giác của góc BAC nên DAB^=DAC^=1/2BAC^=60o
AD//MC(gt),do đó AMCˆ=DABˆ=60o(hai góc nằm trong vị trí đồng vị)
AMC^=CAD^=60o(hai góc nằm trong vị trí sole trong)
Tam giác AMC có hai góc bằng nhau và khoảng 60o nên là tam giác đều
d)Ta có AF=AC-FC=CM-FC=m-n.
AD
2 tháng 5 2023
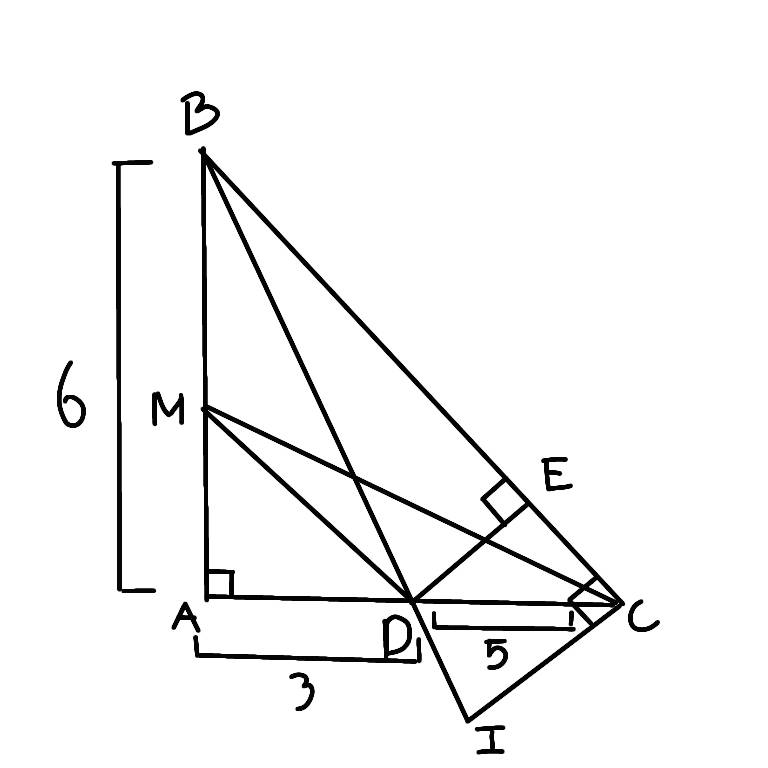a. Tính BC
BC^2 = AC^2 + AB^2
BC^2 = 6^2 + ( AD + DC )^2 = 8^2
BC^2 = 36 + 64 = 100
BC = căng bậc 100 = 10 cm
Tính tỉ số diện tích
Xét tam giác ABC có MD // BC
tam giác AMD ~ tam giác ABC
=>Diện tích tam giác AMD / Diện tích tam giác ABC = (AD/AC)^2=(3/8)^2=9/16 cm2
b.Xét tam giác AMD và tam giác EDC có
Góc MAD = góc CED = 90° (gt)
Góc D chung
=> tam giác AMD ~ tam giác EDC (g.g)
=>MD/AD = DC/EC
=>MD.EC=AD.DC
c. Xét tam giác BCI và tam giác BDE có
Góc BCI = Góc BED = 90°(gt)
Góc B chung
=> Tam giác BCI ~ tam giác BDE(g.g)
=> BC/BI = BD/BE
=> BC.BE = BI.BD(1)
Xét tam giác CBA và tam giác CDE có
Góc CAB = góc CED =90° (gt)
Góc C chung
=> Tam giác CBA ~ tam giác CDE(g.g)
=> CB/CA=CD/CE
=> CB.CE = CA.CD(2)
Từ (1) và (2) ta cộng cho 2 vế
=>BC.BE + CB.CE = BD.BI + CA.CD
=>(BE+CE)BC = BD.BI + CA.CD
=> BC.BC = BD.BI + CA.CD
=> BC^2 = BD.BI + CA.CD
CM
4 tháng 1 2017
a) Xét tứ giác ADME có:
∠(DAE) = ∠(ADM) = ∠(AEM) = 90o
⇒ Tứ giác ADME là hình chữ nhật (có ba góc vuông).
b) Ta có ME // AB ( cùng vuông góc AC)
M là trung điểm của BC (gt)
⇒ E là trung điểm của AC.
Ta có E là trung điểm của AC (cmt)
Chứng minh tương tự ta có D là trung điểm của AB
Do đó DE là đường trung bình của ΔABC
⇒ DE // BC và DE = BC/2 hay DE // MC và DE = MC
⇒ Tứ giác CMDE là hình bình hành.
c) Ta có DE // HM (cmt) ⇒ MHDE là hình thang (1)
Lại có HE = AC/2 (tính chất đường trung tuyến của tam giác vuông AHC)
DM = AC/2 (DM là đường trung bình của ΔABC) ⇒ HE = DM (2)
Từ (1) và (2) ⇒ MHDE là hình thang cân.
d) Gọi I là giao điểm của AH và DE. Xét ΔAHB có D là trung điểm của AB, DI // BH (cmt) ⇒ I là trung điểm của AH
Xét ΔDIH và ΔKIA có
IH = IA
∠DIH = ∠AIK (đối đỉnh),
∠H1 = ∠A1(so le trong)
ΔDIH = ΔKIA (g.c.g)
⇒ ID = IK
Tứ giác ADHK có ID = IK, IA = IH (cmt) ⇒ DHK là hình bình hành
⇒ HK // DA mà DA ⊥ AC ⇒ HK ⊥ AC
a: Ta có: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
hay DB=DC
c: Xét ΔKDC có \(\widehat{KDC}=\widehat{KCD}\left(=\widehat{B}\right)\)
nên ΔKDC cân tại K
Còn câu b nữa bạn 🙂