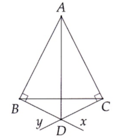
Cho tam giác ABC cân tại A. Trên nửa mặt phẳng bờ BC không chứa A lần lượt vẽ các tia Bx cà Cy sao cho Bx ⊥ BA; Cy ⊥ CA. Gọi D là giao điểm của Bx và Cy. Chứng minh:
a) ΔABD = ΔACD;
b) DA là tia phân giác của góc BDC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 11 2019
Do tam giác ABC cân tại A nên AB = AC, từ đó tam giác ABD = tam giác ACD (cạnh huyền - cạnh góc vuông).
22 tháng 11 2023
Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD
10 tháng 9 2020
Xét 2 tam giác ABD vuông tại B và tam giác ACD vuông tại C có:
+ Chung cạnh huyền AD
+ AB=AC vì tam giác ABC cân tại A
Vậy 2 tam giác ABD bằng tam giác ACD theo trường hợp (cạnh huyền - cạnh góc vuông)
11 tháng 7 2019
a) Xét tam giác vuông ABM và tam giác vuông NCA có:
NC=AB( gt)
CA=BM ( gt)
=> Tam giác ABM = Tam giác NCA
b) Xét tam giác vuông NCA và tam giác vuông BAC có:
AC chung
NC=BA
=> Tam giác NCA =Tam giác BAC
=> ^NAC =^BCA
mà hai góc trên ở vị trí so le trong
=> NA//BC (1)
c) Xét tam giác vuông ABC và tam giác vuông BMA có:
AB chung
AC=BM
=> Tam giác vuông ABC = Tam giác vuông BMA
=> ^MAB=^ABC
mà hai góc trên ở vị trí so le trong
=> MA//CB (2)
từ (1) , (2) => N, A, M thẳng hàng
Ta lại có: NA=AM ( Tam giác ABM =tam giác NCA)
=> A là trung điểm MN
a) Xét Δ ABD vuông tại B và Δ ACD vuông tại C có:
+ AD chung.
+ AB = AC (Tam giác ABC cân tại A).
\(\Rightarrow\Delta ABD=\Delta ACD\) (cạnh huyền - cạnh góc vuông).
b) \(\Delta ABD=\Delta ACD\left(cmt\right).\Rightarrow\) \(\widehat{BDA}=\widehat{CDA}\) (2 góc tương ưng).
\(\Rightarrow\) DA là tia phân giác của \(\widehat{BDC}.\)