tam giác abc vuông tại a. Trên cạnh BC lấy 2 điểm m và n sao cho BM=BA; CN=CA.Số đo MAN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trước tiên, ta có BM = BC theo đề bài. Vì tam giác ABC vuông tại A, nên ta có góc BAC = 90 độ.
Tiếp theo, ta biết rằng phân giác tam giác ABC cắt AC tại K. Vì vậy, ta có góc BAK = góc CAK.
Tương tự, phân giác tam giác ABC cắt MC tại I, nên ta có góc BAM = góc CAM.
Vì CN = MA, nên ta có góc CAN = góc CMA.
Từ các quan sát trên, ta có thể thấy rằng góc BAK = góc BAM = góc CAN = góc CMA.
Vì vậy, ta có thể kết luận rằng K, M, N thẳng hàng.
BN+NC=BC
BA+AM=BM
mà BC=BM và NC=AM
nên BN=BA
Xét ΔBAK và ΔBNK có
BA=BN
góc ABK=góc NBK
BK chung
Do đó: ΔBAK=ΔBNK
=>góc BNK=90 độ và KA=KN
Xét ΔKAM vuông tại A và ΔKNC vuông tại N có
KA=KN
AM=NC
Do đó; ΔKAM=ΔKNC
=>góc AKM=góc NKC
=>góc AKM+góc AKN=180 độ
=>K,M,N thẳng hàng

*lâu r ms lm hình:DD*
+,Có `BK` là p/g `=>hat(B_1)=hat(B_2)`
Có `BM=BC` và `AM=NC` (\(gt\))
`=>BM-AM=BC-NC`
hay `BA=BN`
Xét `Delta ABK` và `Delta NBK` có :
`{:(BK-chung),(hat(B_1)=hat(B_2)(cmt)),(BA=BN(cmt)):}}`
`=>Delta ABK = Delta NBK(c.g.c)`
`=>{(hat(A_1)=hat(N_1)(tương.ứng)(1)),(AK=NK(tương.ứng)):}`
+, Từ `(1)` ; `hat(A_1)+hat(A_2)=180^0` (kề bù) ; `hat(N_1)+hat(N_2)=180^0` (kề bù)
`=>hat(A_2)=hat(N_2)`
Xét `Delta AKM` và `Delta NKC` có :
`{:(AK=NK(cmt)),(hat(A_2)=hat(N_2)(cmt)),(AM=NC(Gt)):}}`
`=>Delta AKM=Delta NKC (c.g.c)`
`=>hat(K_1)=hat(K_2)` ( 2 góc tương ứng )
`=>hat(K_1)+hat(AKN)=hat(K_2)+hat(AKN)`
hay `hat(MKN)=hat(CKA)`
mà `hat(CKA)=180^0` (`K in AC` )
Nên `hat(MKN)=180^0`
`=>M ; K ; N` thẳng hàng
Hình :
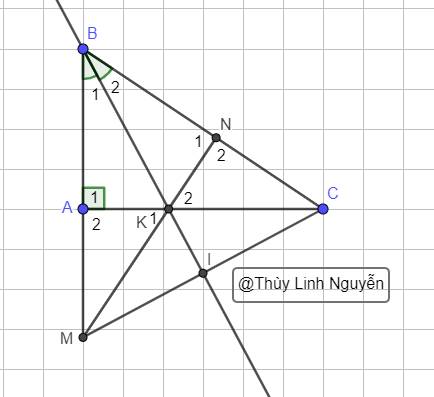

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}\)
\(\Leftrightarrow\widehat{ACB}=90^0-60^0\)
hay \(\widehat{ACB}=30^0\)
Vậy: \(\widehat{ACB}=30^0\)
b) Xét ΔADB và ΔEDB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔADB=ΔEDB(c-g-c)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(đpcm)
c) Ta có: BE+EC=BC(E nằm giữa B và C)
BA+AM=BM(A nằm giữa B và M)
mà BE=BA(ΔBED=ΔBAD)
và BC=BM(gt)
nên EC=AM
Xét ΔADM vuông tại A và ΔEDC vuông tại E có
DA=DE(ΔDAB=ΔDEB)
AM=EC(cmt)
Do đó: ΔADM=ΔEDC(hai cạnh góc vuông)
nên \(\widehat{ADM}=\widehat{EDC}\)(hai góc tương ứng)
mà \(\widehat{EDC}+\widehat{ADE}=180^0\)(hai góc kề bù)
nên \(\widehat{ADM}+\widehat{ADE}=180^0\)
\(\Leftrightarrow\widehat{EDM}=180^0\)
hay E,D,M thẳng hàng(đpcm)

nếu ABC la tg vuong can tai A thi goc MAN =30o
bạn xem lại đề coi


Bài 1: Tính tổng các số có 3 chữ số
a) Chia hết cho 7.
b) Chia hết cho 8
Bài 2: Tính tổng các số có 3 chữ số
a) Chia cho 5 dư 1.
b) Chia cho 4 dư 2
c) Chia 6 dư 2
Bài 3: Để đánh số trang một quyển sách dày 235 trang cần dùng bao nhiêu chữ số.
Bài 4 : Không thực hiện phép tính hãy cho biết các tích sau tận cùng là bao nhiêu chữ số 0.
a) 1 x 2 x 3 x 4 x 5 x ……… x 20 x 21
b) 1 x 2 x 3 x 4 x 5 x ……. X 47 x 48.
làm hộ tui nữa nha

1: Xét ΔBAM và ΔBNM có
BA=BN
góc ABM=goc NBM
BM chung
Do đó: ΔBAM=ΔBNM
2: ΔBAM=ΔBNM
=>MA=MN
mà BA=BN
nên BM là trung trực của AN
=>I là trung điểm của AN
3: góc ABC+góc C=90 độ
góc NMC+góc C=90 độ
=>góc ABC=góc NMC

Ta có
BM=AB suy ra tam giác BAM cân tại B suy ra \(\widehat{BAM}=\frac{180^o-\widehat{B}}{2}\)
CN=AC suy ra tam giác NAC cân tại C suy ra \(\widehat{NAC}=\frac{180^o-\widehat{C}}{2}\)
(nếu cần thì bạn phải cm thêm cả N nằm giữa B và M nhé!)
MÀ ta thấy \(\widehat{BAM}+\widehat{ACN}=\widehat{BAC}+\widehat{NAM}\)
\(\Rightarrow\frac{180^o-\widehat{B}}{2}+\frac{180^o-\widehat{C}}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\frac{360^o-90^o}{2}=90^o+\widehat{NAM}\)
\(\Rightarrow\widehat{NAM}=45^o\)
\(\Delta BAM\) có BA = BM => \(\Delta BAM\) cân tại B
=> \(\widehat{BAM}=\widehat{BMA}\)
\(\Delta CAN\) có CN = CA => \(\Delta CAN\) cân tại C
=> \(\widehat{CAN}=\widehat{CNA}\)
Suy ra:
\(\left\{{}\begin{matrix}\widehat{AMN}=\dfrac{180^o-\widehat{B}}{2}\\\widehat{ANM}=\dfrac{180^o-\widehat{C}}{2}\end{matrix}\right.\Rightarrow\widehat{AMN}+\widehat{ANM}=\dfrac{180^o-\widehat{B}+180^o-\widehat{C}}{2}=\dfrac{360^o-\left(\widehat{B}+\widehat{C}\right)}{2}=\dfrac{360^o-\left(180^o-90^o\right)}{2}=\dfrac{360^o-90^o}{2}=135^o\)
\(\Rightarrow\widehat{MAN}=180^o-135^o=45^o\)