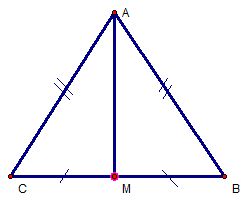
1. Cho tam giac ABC co trung tuyen AM. Goi BD la duong cao cua tam giac ABM; CE la duong cao cua tam giac ACM.
a. Chung minh BD= CE
b. Goi S va T lan luot la trung diem cua BM, MC. Chung minh: DS= ET
2. Cho tam giac ABC can ( AB= AC), ve duong cao AH va BK cat nhau tai E. Chung minh.
a. tg ABK= tg BAH
b. tg AEB can
c. AE la duong trung truc
3. Cho tam giac CDE can tai C, duong cao CH. TU H ke HK vuong goc CD va HF vuong goc CE.
a. Chung minh: CH la duong trung truc cua KF
b. Tren tia doi HK lay diem M sc MH= HK. Chung minh EM vuong goc HK
4. Cho tam giac ABC. Tren AB lay hai diem D va E sc AD= DE= EB. Goi AI la trung tuyen cua tam giac ABC va M la giao diem cua AI va CD
a. Chung minh: M la trung diem cua AI
b. Chung minh DM=\(\dfrac{1}{4}\)DC
Giup mk vs hom nay nop rui![]()
![]()
![]()
![]()
![]()
![]()