Cho hình thang ABCD (AB//CD) có AB = 9cm; CD = 11cm. Đường trung bình MN có độ dài bằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VN
0
LN
0
1 tháng 7 2018
Ta áp dụng công thức Brahmagupta để tính
\(s=\frac{\sqrt{\left(AB^2+CD^2+BD^2+AC^2\right)+8\cdot AB\cdot CD\cdot BD\cdot AC-2\left(AB^4+CD^4+BD^4+AC^4\right)}}{4}\)
A) Thay số vào ta đc \(S=6\sqrt{55}\approx44,4972\left(cm^2\right)\)
b) \(S\approx244,1639\left(cm^2\right)\)
hok tốt ...
CN
26 tháng 7 2019
Công thức Brahmagupta là công thức tính diện tích của một tứ giác nội tiếp (tứ giác mà có thể vẽ một đường tròn đi qua bốn đỉnh của nó) mà hình thang ko có đường tròn nào đi qua đủ bốn đỉnh của nó nên công thức này ko được áp dụng vào bài này
A
21 tháng 1 2021
Kẻ BK ^CD tại K Þ AB = HK
S A B C D = ( 2 H K ) + 2 K C ) . A H 2 = H C . A H = 96 c m 2
21 tháng 1 2021
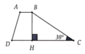
Kẻ BH \(\perp\) CD tại H
Xét tam giác BHC vuông tại H (BH \(\perp\) CD): \(\widehat{C}\) = 30o
\(\Rightarrow\) BH = \(\dfrac{1}{2}\)BC (Tính chất cạnh đối diện với góc 30o bằng một nửa cạnh huyền)
hay BH = \(\dfrac{1}{2}\).8 = 4(cm)
Vì ABCD là hình thang (AB // CD)
\(\Rightarrow\) SABCD = \(\dfrac{1}{2}\)(AB + CD).BH = \(\dfrac{1}{2}\).(2 + 9).4 = 22 (cm2)
Chúc bn học tốt!
NT
1
6 tháng 7 2017
Vì BC = AD suy ra BC = 5cm.Kẻ một đường chéo từ B đến D. Ta có 2 tam giác ADB và BCD.
Diện tích hình thang ABCD là : 9 x 5 : 2 + 17 x 5 : 2 = 65(cm2)
10 cm
\(MN=\dfrac{AB+CD}{2}=\dfrac{9+11}{2}=10\left(cm\right)\)