Vẽ hình hộ mik
Cho tam giác ABC cân tại A; BD vuông góc AC; CE vuông góc AB; BD giao CE ở H .
CM : a) BD=CE
b) tam giác HEB = HDC
c) AH là phân giác góc BAC
d) AH vuông góc BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
17 tháng 4 2019
Hình = tự vẽ .-.
a) ∠BAC = ?
Vì ΔABC cân tại A nên:
∠BAC = 180° - 2∠ABC = 180° - 2. 36° = 180° - 72° = 108°
b) ΔABE = ΔABF
Xét ΔBCE vuông tại E:
∠EBC + ∠ECB = 90° ⇒ ∠EBC = 90° - 36° = 54°
⇒ ∠EBA + ∠ABC = ∠EBC = 54° ⇒ ∠EBA = 54° - ∠ABC = 54° - 36° = 18° (1)
Vì BD là phân giác của ∠ABC nên:
∠ABD = ∠CBD = ∠ABC : 2 = 36° : 2 = 18° (2)
Từ (1) và (2) suy ra: ∠EBA = ∠ABD (=18°)
Xét hai tam giác vuông ABE và ABF có:
AB: cạnh chung
∠EBA = ∠ABD (cmt)
Do đó: ΔEBA = ΔABF (cạnh huyền - góc nhọn)
12 tháng 3 2022
a, Xét tam giác AHB và tam giác AHC có
AH _ chung
AB = AC
Vậy tam giác AHB~ tam giác AHC (ch-cgv)
Ta có tam giác ABC cân tại A, có AH là đường cao
đồng thười là đường pg
b, Xét tam giác AMH và tam giác NAH có
HA _ chung
^MAH = ^NAH
Vậy tam giác AMH = tam giác NAH (ch-gn)
=> AM = AN ( 2 cạnh tương ứng )
c, Ta có AM/AB = AN/AC => MN // BC
d, Ta có \(AH^2+BM^2=AN^2+BH^2\)
Xét tam giác BMH vuông tại M \(MB^2=BH^2-MH^2\)
Thay vào ta được \(AH^2+BH^2-MH^2=AN^2+BH^2\Leftrightarrow AH^2-MH^2=AN^2\)
Lại có AM = AN (cmt)
\(AM^2=AH^2-MH^2\)( luôn đúng trong tam giác AMH vuông tại M)
Vậy ta có đpcm
CM
29 tháng 4 2018
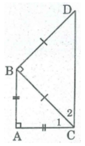
Vì ΔABC vuông cân tại A nên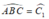 
Lại có: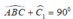 
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên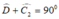 
Lại có: 
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.
a) Xét hai tam giác vuông ABD và ACE có:
AB = AC (GT)
ˆBAC:chungBAC^:chung
=> ABD = ACE (c.h - g.n)
b) Ta có: ΔABC cân tại A có AH là đường cao
=> AH là đường trung tuyến của BC
=> H là trung điểm của BC
=> BH = CH = BC : 2 (1)
ΔDBC vuông tại D có DH là đường trung tuyến của BC
=> DH là đường trung tuyến ứng vs cạnh huyền
=> DH = BC : 2 (2)
Từ (1) và (2) => CH = DH
=> Tam giác HDC cân tại H
c/ Xét 2 tam giác vuông ΔHDM và ΔHCM ta có:
Cạnh huyền DH = CH (cmt)
HM: chung
=> ΔHDM = ΔHCM (c.h - c.g.v)
=> DM = CM (2 cạnh tương ứng)
d/ Đang suy nghĩ ạ :((