Cho tam giác ABC vuông tại A, P/g BD và CE cắt nhau tại I . Biết AD = 2 ; BD = 3 . tính DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

HT
14 tháng 7 2017
( bạn tự vẽ hình nha )
a) AB2= BC2 - AC2 ( Py ta go ) => AB = 6
Áp dụng tính chất đương phân giác ta có : \(\frac{AB}{BC}=\frac{AD}{DC}=\frac{6}{10}=>10AD=6DC\)( mà AD = 8- DC (1) )
=> 10( 8- DC ) = 6x DC
=> 80-10DC = 6DC
=> 80= 16DC => DC = 5 => AD = 8-5 = 3
Vậy AD = 3 ; DC = 5

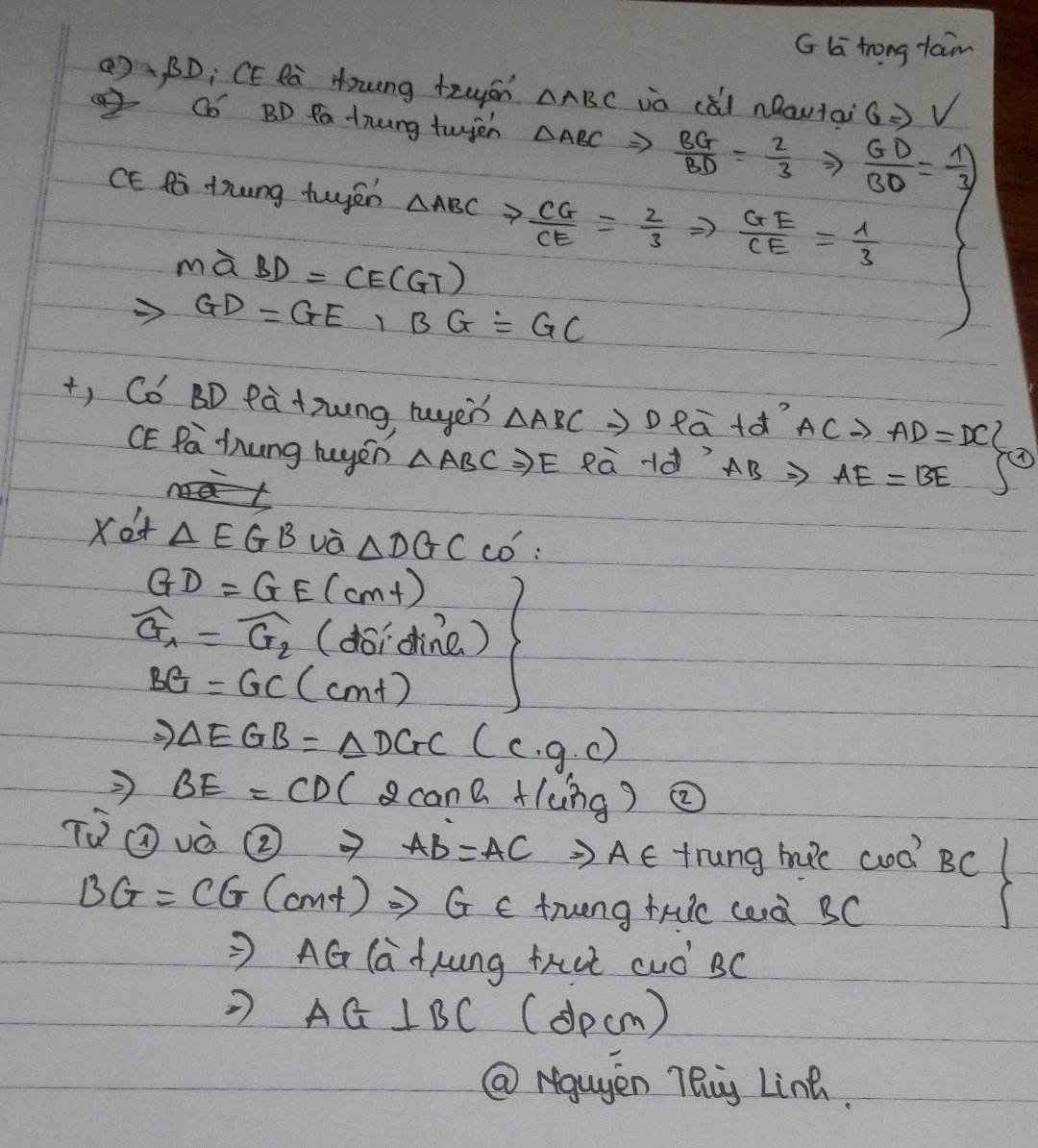
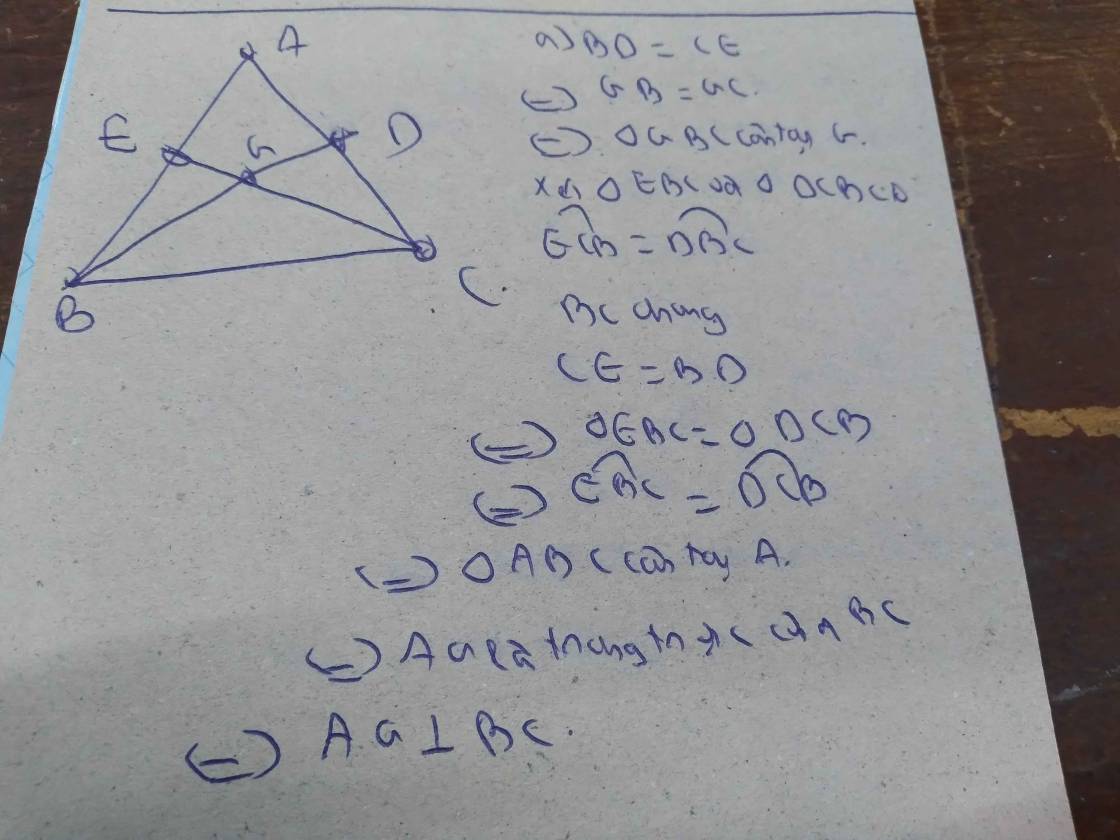
A B C E D I
Áp dụng ĐL Pi ta go trong tam giác vuông ABD có: AB2 = BD2 - AD2 = 9 - 4 = 5 => AB = \(\sqrt{5}\)
BD là phân giác của góc BAC => \(\frac{AD}{AB}=\frac{DC}{BC}\) => \(\frac{DC}{BC}=\frac{2}{\sqrt{5}}\) => DC = \(\frac{2}{\sqrt{5}}\). BC
AC = AD + DC = 2 + \(\frac{2}{\sqrt{5}}\). BC
Áp dụng ĐL pia ta go trong tam giác ABC có: AB2 + AC2 = BC2
=> 5 + (2 + \(\frac{2}{\sqrt{5}}\). BC )2 = BC2
=> 5 + 4 + \(\frac{8}{\sqrt{5}}\). BC + \(\frac{4}{5}\)BC2 = BC2
=> 45 + 8\(\sqrt{5}\). BC - BC2 = 0
=> BC = 9\(\sqrt{5}\) => AC = 20
+) Vì CE là p/g của góc ACB nên \(\frac{AE}{BE}=\frac{AC}{BC}=\frac{20}{9\sqrt{5}}\)=> \(\frac{AE}{BE+AE}=\frac{20}{9\sqrt{5}+20}\Rightarrow\frac{AE}{\sqrt{5}}=\frac{20}{9\sqrt{5}+20}\)
=> AE = \(\frac{20\sqrt{5}}{9\sqrt{5}+20}=\frac{20}{9+4\sqrt{5}}\)
Áp dụng ĐL Pi ta go trong tam giác ADE có: DE2 = AE2 + AD2 = \(\frac{20^2}{\left(9+4\sqrt{5}\right)^2}+4\)
=> DE = \(\frac{\sqrt{400+4\left(9+4\sqrt{5}\right)^2}}{9+4\sqrt{5}}=..\)