Cho đường tròn tâm O, bán kính R với đường kính AB, hai dây AD & BC cắt nhau ở E nằm trong đường tròn
C/mR : AE.AD+BE.BC=4xR^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)

C A B D H O
AB = 10cm
BC= 12 cm
Gọi \(H=AD\) \(\Omega\) \(BC\)
Ta có AD vuông góc với BC mà ADlà đường kính
\(\Rightarrow\)AD là đường trung trực của BC
\(\Rightarrow\)H là ttrung điểm \(\Rightarrow HC=HB=\frac{1}{2}.BC=6cm\)
Tam giác ABC vuông tại H
\(\Rightarrow AH=\sqrt{AB^2-HB^2}=8cm\)
Tam giác ABD vuông tại B (chắn nửa đương tròn )
\(\Rightarrow AD=\frac{AB^2}{AH}=\frac{10^2}{8}=12,5cm\)
\(\Rightarrow R=\frac{1}{2}.AD=6,25cm\)
Vậy bán kính của đườn tròn là : \(6,25cm\)
Chúc bạn học tốt !!!

b.
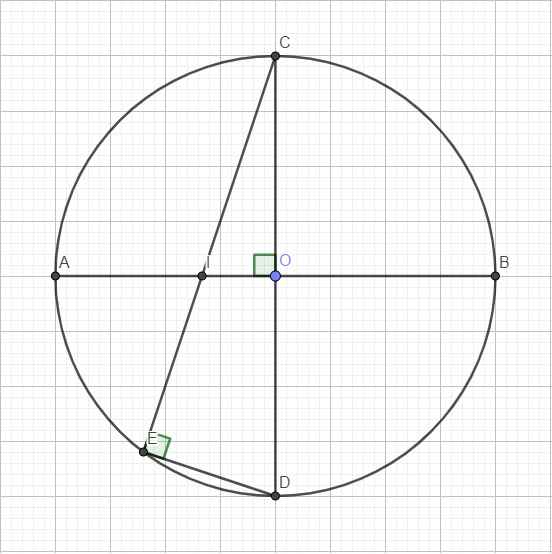
Áp dụng định lý Pitago trong tam giác vuông COI:
\(CI=\sqrt{OC^2+OI^2}=\sqrt{R^2+\left(\dfrac{R}{3}\right)^2}=\dfrac{R\sqrt{10}}{3}\)
Do 2 tam giác COI và CED đồng dạng
\(\Rightarrow\dfrac{CE}{CO}=\dfrac{CD}{CI}\Rightarrow CE=\dfrac{CD.CO}{CI}=\dfrac{2R.R}{\dfrac{R\sqrt{10}}{3}}=\dfrac{3R\sqrt{10}}{5}\)
http://olm.vn/hoi-dap/question/74826.html