Cho tứ diện S.ABC có đáy ABC là tam giác vuông tại B với AB = 3; BC = 4. Hai mặt bên (SAB) và (SAC) cùng vuông góc với (ABC) và SC hợp với (ABC) góc 45 o . Tính thể tích hình cầu ngoại tiếp S.ABC.
A. V = 5 π 2 3
B. V = 25 π 2 3
C. V = 125 π 3 3
D. V = 125 π 2 3


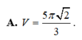
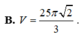
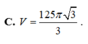
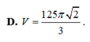
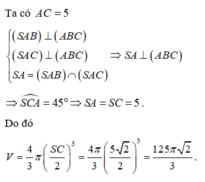

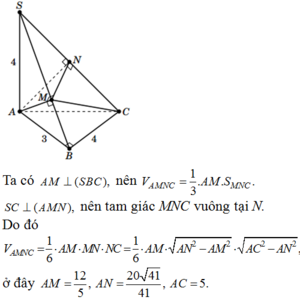
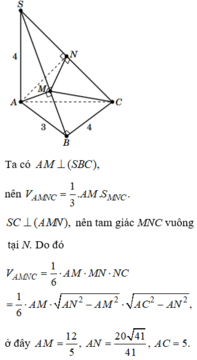
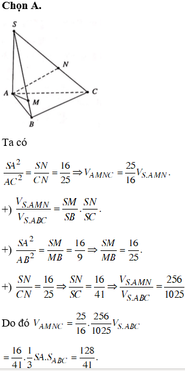

Ta có AC = 5
S A B ⊥ A B C S A C ⊥ A B C S A = S A B ∩ S A C ⇒ S A ⊥ A B C ⇒ S C A ^ = 45 o ⇒ S A = S C = 5
Do đó
V = 4 3 π SC 2 3 = 4 3 π 5 2 2 3 = 125 π 2 3
Đáp án D