Cho hình thoi ABCD có AC = 20; BAD = 60. N là một điểm nằm trên gọi P; Q lần lượt là hình chiếu vuông góc củ N lên BD và AC.
a. Tính diện tích hình thoi ABCD.
b. Tính độ dài nhỏ nhất của đoạn PQ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

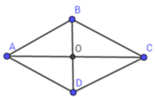
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A

Lời giải:
Độ dài đường chéo BD của hình thoi:
$20\times 2:10=4$ (cm)

Độ dài đường chéo BD là :
\(20\times\dfrac{3}{5}=12\left(cm\right)\)
Diện tích hình thoi ABCD là :
\(\dfrac{20\times12}{2}=120\left(cm^2\right)\)
Đ/S : \(120cm^2\)

giải
Đường chéo BD là:
20x2/5=8(cm)
Diện tích hình thoi là:
20x8:2=80(\(cm^2\))
Đ/S:80 \(cm^2\)

Đáp án B
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
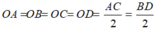
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.

A B C D O AC = 8 BD = 6
Gọi \(O\) là giao điểm của \(AC\)và \(BD\).
Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)
Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)
Áp dụng định lí Pitago trong \(\Delta AOB\) có:
\(AB^2=AO^2+OB^2\)
\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)
\(\Rightarrow AB=5cm\)
\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)
Vậy ...............

Ta có: \(S_{ABCD}=\dfrac{1}{2}.BD.AC\)(với S là diện tích)
\(\Rightarrow\dfrac{1}{2}.2a.8a=32\)
\(\Rightarrow8a^2=32\)
\(\Rightarrow a^2=4\)
\(\Rightarrow a=2\left(cm\right)\)
Mọi người giúp mình với.