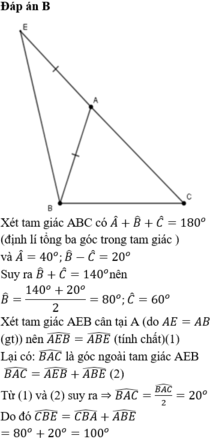
Tam giác ABC có A ^ = 40 o ; B ^ - C ^ = 20 o . Trên tia đối của tia AC lấy điểm E sao cho AE=AB. Tính số đo góc CBE
A. 80 °
B. 100 °
C. 90 °
D. 120 °
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Do \(\widehat{A}=100^0>90^0\) nên là góc tù, do đó, \(\widehat{A}\) là góc lớn nhất trong tam giác ABC.
\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)
b)
Theo định lí tổng 3 góc trong tam giác ABC, ta có:
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}\)
\( \Rightarrow\widehat C = \widehat B = {40^o}\)
\( \Rightarrow \) ABC là tam giác cân tại A.


Đáp án:
ΔAMB: ∠B = 70o70o; ∠AMB = 90o90o; ∠BAM = 20o20o
ΔAMC: ∠C = 70o70o; ∠AMC = 90o90o; ∠CAM = 20o20o
Giải thích các bước giải:
ΔABC có AB = AC ⇔ ΔABC cân tại A ⇔ ∠B = ∠C
Mà ∠BAC = 40o40o ⇒ ∠B + ∠C = 140o140o
⇒ ∠B = ∠C = 70o70o
Xét ΔAMB và ΔAMC có:
AB = AC (gt)
AM: cạnh chung
MB = MC (M là trung điểm của BC)
⇒ ΔAMB = ΔAMC (c.c.c)
⇒ ∠AMB = ∠AMC (2 góc tương ứng)
∠BAM = ∠CAM (2 góc tương ứng)
Lại có: ∠AMB + ∠AMC = 180o180o (2 góc kề bù)
⇒ ∠AMB = ∠AMC = 180o2180o2 = 90o90o
∠BAM + ∠CAM = ∠BAC = 40o40o
⇒ ∠BAM = ∠CAM = 40o240o2 = 20o20o

Bài 1:
Xét \(\Delta ABC\) có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(ĐL tổng 3 góc 1 \(\Delta\))
\(\Rightarrow30^o+70^o+\widehat{C}=180^o\) (Vì \(\widehat{A}=30^o;\widehat{B}=70^o\) (gt))
\(\Rightarrow\widehat{C}=180^o-30^o-70^o=80^o\)
Bài 2:
Xét \(\Delta ABC\) (vuông tại A) có:
\(\widehat{B}+\widehat{C}=90^o\) (Tc \(\Delta\) vuông)
\(\Rightarrow\widehat{B}+40^o=90^o\) (Vì \(\widehat{C}=40^o\) (gt))
\(\Rightarrow\widehat{B}=90^o-40^o=50^o\)
Giải:
+) Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) ( 3 góc của tam giác )
\(\Rightarrow30^o+70^o+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=80^o\)
Vậy...
+) Ta có: \(\widehat{B}+\widehat{C}=90^o\) ( do tam giác có \(\widehat{A}=90^o\) )
\(\Rightarrow40^o+\widehat{B}=90^o\)
\(\Rightarrow\widehat{B}=50^o\)
Vậy...

`a,` vì Tam giác `ABC` có \(\widehat{A}=110^0\)
`=>` Tam giác `ABC` là tam giác tù.
`b,` Cạnh đối diện của \(\widehat{A}\) là cạnh `BC`
`=>` Cạnh lớn nhất của Tam giác `ABC` là cạnh `BC`