Cho hình thang ABCD ( AB // CD) . Biết AB = 3 cm; AD = 4 cm ; BD = 6cm và góc DAB= góc DBC
a.Chứng minh tam giác ADB đồng dạng tam giác BCD
b.Tính độ dài BC và CD.
c.Tính tỉ số diện tích của hai tam giác ADB và BCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 12 2018
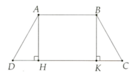
Gợi ý: Kẻ AH ^ CD tại H, kẻ BK ^ CD tại K
Tính được SABCD = 180cm2
19 tháng 8 2021
Bài 8:
a: Xét ΔDBC có
E là trung điểm của BD
M là trung điểm của BC
Do đó: EM là đường trung bình của ΔDBC
Suy ra: EM//DC
b: Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
19 tháng 8 2021
Bài 5:
Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
CM
26 tháng 5 2018
Kẻ BK ^CD tại K Þ AB = HK
S A B C D = ( 2 H K ) + 2 K C ) . A H 2 = H C . A H = 96 c m 2
D
0
29 tháng 8 2018
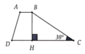
từ A kẻ đường thẳng song song với BC cắt CD tại E
\(\Rightarrow\)tứ giác ABCE là hình bình hành \(\Rightarrow\)AB=CE=4cm;AE=BC=5cm\(\Rightarrow\)DE=CD-EC=4cm
xét \(\Delta\) ADE có:AD2+DE2=32+42=25
AE2=52=25\(\Rightarrow\)AD2+DE2=AE2
\(\Rightarrow\Delta\)ADE vuông tại D \(\Rightarrow AD\perp DE\) hay \(AD\perp DC\)
\(\Rightarrow\)tứ giác ABCD là hình thang vuông
CM
4 tháng 1 2020
a) Chứng minh
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2
CM
16 tháng 2 2017
Đáy lớn hình thang ABCD là : 18 x 3/2 = 27 (cm)
Độ dài đoạn MB là : 18 – 12 = 6 (cm)
MB chính là đáy của ∆ MBC,chiều cao của ∆ MBC ( cũng là chiều cao của hình thang AMCD)
42 × 2 6 = 14 (cm)
Diện tích hình thang AMCD là :
( 12 + 27 ) × 14 2 = 273 (cm2)
Đáp số 273 cm2
a. vì AB//CD => góc ABD=góc BDC
xét tam giác ADB và tam giác BCD có:
góc DAB=góc DBC (gt)
góc ABD= góc BDC (cmt)
=> tam giác ADB ~ tam giác BCD (c.c)
b. vì tam giác ADB ~ tam giác BCD
=> \(\dfrac{AD}{BC}\)=\(\dfrac{AB}{BD}\)=\(\dfrac{DB}{CD}\)
=> BC= \(\dfrac{AD.BD}{AB}\)= \(\dfrac{4.6}{3}\)= 8(cm)
=> CD= \(\dfrac{BD^2}{AB}\)= \(\dfrac{6^2}{3}\)= 12 (cm)