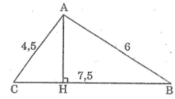
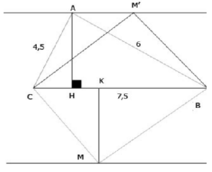
cho tam giác ABC: AB =4,5cm ; AC=6cm ;BC=7,5cm a) chứng tỏ rằng BC²=AB²+AC² b) tam giác ABC là tam giác gì? Vì sao? c) vẽ trung tuyến AM, kẻ AH vuông AC.Trên tia đối của MH lấy điểm K sao cho MK=MH chứng minh : tam giác MHC = tam giác MKB d) chứng minh : BK //AC
Bạn nào giúp mình với chiều mình phải nộp rồi

a: \(BC^2=7.5^2=56.25\)
\(AB^2+AC^2=4.5^2+6^2=56.25\)
Do đó: \(BC^2=AB^2+AC^2\)
b: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét ΔMHC và ΔMKB có
MH=MK
\(\widehat{HMC}=\widehat{KMB}\)
MC=MB
Do đó: ΔMHC=ΔMKB