cho tam giác ABC có AB=8CM ; AC=6CM và BC=10CM . Chứng minh rằng tam giác ABC là tam giác vuông tại A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
1
9 tháng 3 2022
Xét \(\Delta ABC:\)
\(BC^2=10^2=100.\\ AB^2+AC^2=6^2+8^2=100.\\ \Rightarrow BC^2=AB^2+AC^2.\)
\(\Rightarrow\Delta ABC\) vuông tại A (Pytago đảo).
L
2
11 tháng 10 2023
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=\dfrac{1}{2}\cdot8\cdot12\cdot sin30=24\left(cm^2\right)\)
CN
1
5 tháng 4 2022
Trường hợp 1: BC=18cm
=>NHận
=>C=AB+BC+AC=36+8=44(cm)
TRường hợp 2: BC=8cm
=>LOại
BN
7 tháng 3 2022
khi muốn bt nó là tam giác gì thì ta thường áp định lí pi-ta-go đảo vào bài đó và thường là xét các cạnh
ta sẽ lấy tổng bình phương hai cạnh nhỏ nhất xem có bằng bình phương cạnh lớn nhất hay ko
áp vào bài này
lấy: 62+82=36+64=100
100=102
Vậy tam giác này là tam giác vuông
PT
1
CM
14 tháng 1 2018
b. Vì AB < AC < BC ⇒ ∠C < ∠B < ∠A (quan hệ giữa góc và cạnh đối diện trong tam giác)
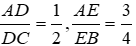
Ta có:
\(AB^2+AC^2=8^2+6^2=64+36=100\left(cm\right)\)
\(BC^2=10^2=100\left(cm\right)\)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A (định lý Pi-ta-go đảo)
Áp dụng định lý Pytago đảo ta có:
AB2+AC2=82+62=100
mà 102=100
⇒82+62=102hay AB2+AC2=BC2
vậy ABC là tam giác vuông tại A