cho góc xoy trên ox lấy hai điểm A và B,trên oy lấy hai điểm Cvà D sao cho oA=oC; AB=CD.Chứng minh rằng
a) tam giác ABC =tam giác CDA
b)tam giácABD= tam giác CDB
xin m.n giúp mình.Cám ơn m.n rất nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔODB và ΔOCA có
\(\dfrac{OD}{OC}=\dfrac{OB}{OA}\left(\dfrac{3}{6}=\dfrac{4}{8}\right)\)
\(\widehat{O}\) chung
Do đó: ΔODB đồng dạng với ΔOCA
=>\(\dfrac{OD}{OC}=\dfrac{OB}{OA}\)
=>\(\dfrac{OD}{OB}=\dfrac{OC}{OA}\)
Xét ΔODC và ΔOBA có
\(\dfrac{OD}{OB}=\dfrac{OC}{OA}\)
\(\widehat{O}\) chung
Do đó: ΔODC đồng dạng với ΔOBA
=>\(\dfrac{DC}{BA}=\dfrac{OC}{OA}\)
=>\(\dfrac{DC}{5}=\dfrac{6}{8}=\dfrac{3}{4}\)
=>\(DC=3\cdot\dfrac{5}{4}=\dfrac{15}{4}=3,75\left(cm\right)\)

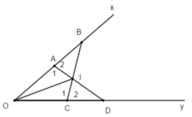
+ Giả sử A nằm giữa hai điểm O và B; C nằm giữa hai điểm O và D
Do đó ta có: OA + AB = OB; OC + CD = OD
Mà OA = OC; OB = OD (gt)
Nên AB = CD
+ Xét tam giác OAD và tam giác OCB có:
OA = OC; OB = OD (gt)
x O y ^ góc chung
Do đó: Δ O A D = Δ O C B (c – g – c)


Đáp án D

Câu hỏi của nguyenvandat - Toán lớp 7 - Học toán với OnlineMath

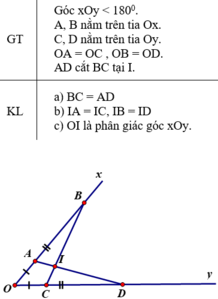
a) ΔAOD và ΔCOB có:
OA = OC (giả thiết)
Góc O chung
OD = OB (giả thiết)
⇒ ΔAOD = ΔCOB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)