Mng ơi giúp em với ạ Cho ( I ; 6cm ) Gọi H là điểm ngoài đường tròn sao cho HI= 12cm. Kẻ 2 tiếp HM, HN (M, N là 2 tiếp điểm) Gọi Q=HI giao nhau MN. a) Chứng minh MN thuộc HT b) Tính QI c) Kẻ đường kính MA chứng minh NA//HI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 2:
uses crt;
var a:array[1..100]of integer;
i,n,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
t:=0;
for i:=1 to n do
if (4<a[i]) and (a[i]<15) then t:=t+a[i];
writeln(t);
readln;
end.


a: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{ABC}=\widehat{ECN}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BD=CE
\(\widehat{MBD}=\widehat{NCE}\)
Do đó: ΔMBD=ΔNCE
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=EN
\(\widehat{MDI}=\widehat{ENC}\)(hai góc so le trong, DM//EN)
Do đó: ΔIDM=ΔIEN
=>IM=IN
=>I là trung điểm của MN

Bài 5:
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y-z}{2+3-4}=\dfrac{-20}{1}=-20\)
Do đó: x=-40; y=-60; z=-80

1. should ask
*must not ask là sai vì người quản lí mới nên hỏi vài câu hỏi trước khi thực hiện thay đổi
*have to ask (mang tính chủ quan) nên có làm hay không làm cũng được nên ta không chọn đáp án này
2. could prevent
Vì sau would, could là V_inf

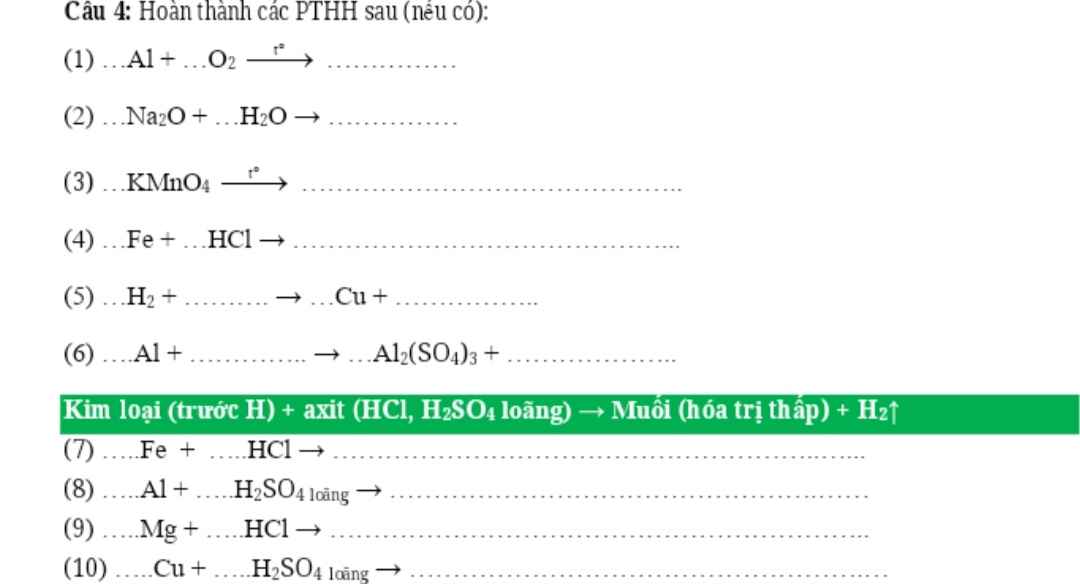
4Al + 3O2 ---> 2Al2O3
Na2O + H2O ---> 2NaOH
2KMnO4 ---> K2MnO4 + MnO2 + O2
Fe + 2HCl ---> FeCl2 + H2
H2 + CuO ---> Cu + H2O
2Al + 3H2SO4 ---> Al2(SO4)3 + 3H2





 mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33 


a: Xét (O) có
HM,HN là tiếp tuyến
nên HM=HN
mà IM=IN
nên IH là trung trực của MN
=>IH vuông góc MN
b: QI=MI^2/IH=6^2/12=3cm
c: Xét (I) có
ΔMNA nội tiếp
MA là đường kính
Do đó: ΔMNA vuông tại N
=>NA vuông góc với NM
=>AN//HI