Tìm giá trị lớn nhất của hàm số trên đoạn [1;3]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C.
• Ta có: y , = 1 2 x + 1 - 1 2 3 - x , cho y , = 0 ⇔ x = 1 ∈ - 1 ; 3
• Tính được: y ( - 1 ) = 2 ; y ( 3 ) = 2 ; y ( 1 ) = 2 2
Vậy m a x y [ - 1 ; 3 ] = 2 2

Đáp án D
Với x ∈ − 2 ; 1 ta có
y = − x 2 + 2 ⇒ y ' = − 2 x ; y ' = 0 ⇔ x = 0.
Ta có y − 2 = − 2 ; y 0 = 2 ; y 1 = 1
Xét x ∈ 1 ; 3 ta có
y = x ⇒ y ' = 1 > 0.
Ta có y 3 = 3
Suy ra max − 2 ; 3 y = 3

Đáp án D
Ta có y ' = 3 x 2 − 4 x + 1 ⇒ y ' = 0 ⇔ x = 1 x = 1 3
Suy ra y − 1 = − 3 , y 1 3 = 31 27 , y 1 = 1 ⇒ max − 1 ; 1 y = 31 27

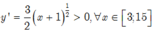
=> Hàm số đã cho đồng biến trên đoạn [ 3; 15].
Hàm số đạt giá trị lớn nhất tại x= 15 và M= y (15) = 64
Chọn A.

Chọn A
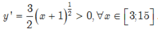
Do đó hàm số đồng biến trên [3; 15]
Hàm số đạt giá trị lớn nhất tại x= 15 và M= y(15)=64.

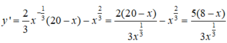
y' = 0 <=> x = 8
Ta có: y(1) = 19, y(8) = 48, y ( 10 ) = 10 5 3 ≈ 46 , 6 > 19
Từ đó:
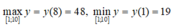
Chọn D

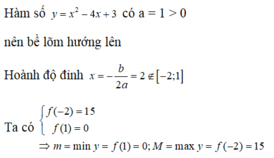

Đáp án B.
Ta có y , = 1 − 4 x 2 ⇒ y , = 0 ⇔ x = ± 2.
Suy ra y 1 = 5 , y 2 = 4 , y 3 = 13 3 ⇒ max 1 ; 3 y = 5.