Có bao nhiêu giá trị nguyên của tham số m ∈ [ -2020; 2020 ] thỏa mãn phương trình : \(x^2+\left(2-m\right)x+1=2\sqrt{x^3+x}\) có nghiệm ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)
CM
20 tháng 6 2019
Đáp án D.
Ta có f ' x = 6 x 2 - 12 x ; f ' x = 0 ⇔ [ x = 0 ⇒ y 0 = 1 - m x = 2 ⇒ y 2 = - 7 - m .
Theo bài ra, ta có y 0 . y 2 < 0 ⇔ 1 - m - 7 - m < 0 ⇔ - 7 < m < 1 .
CM
17 tháng 2 2019
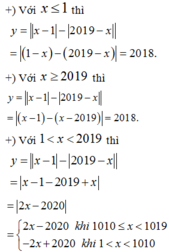
Do đó
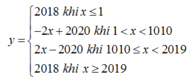
Vẽ dáng đồ thị hàm số ta được:
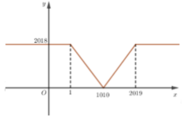
Từ hình vẽ ta thấy phương trình đã cho có nghiệm nếu đường thẳng y = 2020 - m cắt đồ thị hàm số trên tại ít nhất một điểm hay
giá trị của m thỏa mãn bài toán.
Chọn D.
CM
23 tháng 3 2017
Đáp án D.
Đặt
f x = 3 x 4 − 4 x 3 − 12 x 2 → f ' x = 12 x 3 − 12 x 2 − 24 x , ∀ x ∈ ℝ .
Khi đó y = f x + m ⇒ y ' = f ' x . f x + m f x + m .
Phương trình y ' = 0 ⇔ f ' x = 0 f ' x = − m ( * )
Để hàm số đã cho có 7 điểm cực trị
⇔ y ' = 0 có 7 nghiệm phân biệt.
Mà f ' x = 0 có 3 nghiệm phân biệt
⇒ f x = − m có 4 nghiệm phân biệt.
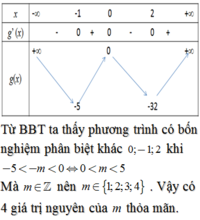
Dựa vào BBT hàm số f x , đẻ (*) có 4 nghiệm phân biệt
⇔ − 5 < − m < 0 ⇔ m ∈ 0 ; 5 .
Kết hợp với m ∈ ℤ suy ra có tất cả 4 giá trị nguyên cần tìm.
CM
10 tháng 12 2019
Đáp án D
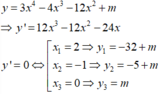
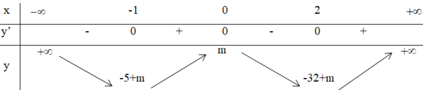
Dựa vào BBT để hàm số y = 3 x 4 − 4 x 3 − 12 x 2 + m có 7 điểm cực trị thì:
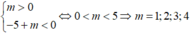
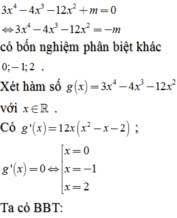
ĐKXĐ: \(x\ge0\)
\(x^2+1+\left(2-m\right)x-2\sqrt{x\left(x^2+1\right)}=0\)
Với \(x=0\) ko phải nghiệm, với \(x>0\) chia 2 vế cho x:
\(\Rightarrow\dfrac{x^2+1}{x}+2-m-2\sqrt{\dfrac{x^2+1}{x}}=0\)
Đặt \(\sqrt{\dfrac{x^2+1}{x}}=t\ge\sqrt{2}\)
\(\Rightarrow t^2-2t+2=m\)
Xét hàm \(f\left(t\right)=t^2-2t+m\) khi \(t\ge\sqrt{2}\)
\(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=1< \sqrt{2}\end{matrix}\right.\) \(\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge\sqrt{2}\)
\(\Rightarrow f\left(t\right)\ge f\left(\sqrt{2}\right)=4-2\sqrt{2}\)
\(\Rightarrow\) Pt có nghiệm khi \(m\ge4-2\sqrt{2}\)