Nếu các số 5+ m; 7+2m; 17+ m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?
A. m=2
B.m =3
C. m= 4
D. m= 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gợi ý:
Ta lấy số đầu làm tử, chính số đó và hai số còn lại làm mẫu, tiếp đến lấy số thứ hai làm tử, hai số kia làm mẫu ... (loại các phân số có mẫu bằng 0).
Lời giải
Ta có: Mẫu số của một phân số phải khác 0.
Do đó m có thể chọn trong các số 0; -3; 5.
n có thể chọn trong các số -3; 5.
Vậy ta có thể viết được các phân số 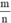 là:
là:
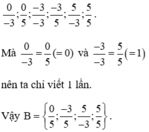

Vì m và n thuộc 0;-3;5 nên n phải khác 0 ( vì m./n là phân số )
Ta có các phân số đó là \(-\frac{3}{5};\frac{0}{3};\frac{0}{5};-\frac{5}{3}\)
Do đó ta có tập hợp \(\left\{\frac{-3}{5};\frac{-5}{3};\frac{0}{5};\frac{0}{3}\right\}\)
Vậy \(B=\left\{-\frac{3}{5};-\frac{5}{3};\frac{0}{3};\frac{0}{5}\right\}\)
\(B=\left\{\frac{0}{-3};\frac{0}{5};\frac{-3}{5};\frac{5}{-3}\right\}\)

Ba số 5 + m ; 7 + 2 m ; 17 + m theo thứ tự u 1 , u 2 , u 3 lập thành cấp số cộng nên
u 1 + u 3 = 2 u 2 ⇔ 5 + m + 17 + m = 2 7 + 2 m ⇔ 2 m + 22 = 14 + 4 m ⇔ − 2 m = − 8 ⇔ m = 4
Chọn đáp án C.