Đồ thị hàm số y = x3 – 3x2 – 9x – 5 có điểm cực tiểu là
A. (3; 32).
B. (-1; 0).
C. x = -1.
D. x = 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Ta có ![]() và y' = 0
và y' = 0 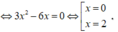
Lập bảng xét dấu ![]()
![]()
Ta thấy y' đổi dấu từ âm sang dương khi đi qua x = 2 nên x = 2 là điểm cực tiểu của hàm số.
Với ![]() suy ra M(2;5) là điểm cực tiểu của đồ thị (C).
suy ra M(2;5) là điểm cực tiểu của đồ thị (C).

Đáp án C.
Ta có: y ' = 3 x 2 + 6 x − 24 = 0 ⇔ x = − 4 ⇒ y = 54 x = 2 ⇒ y = − 54
Do đó điểm cực tiểu của đồ thị hàm số là 2 ; − 54 .

Đáp án D
Ta có y ' = 3 x 2 + 6 x − 9 ; y ' = 0 ⇔ x = 1 x = − 3 . Từ đó 2 điểm cực trị là A 1 ; − 3 ; B − 3 ; 29 . Phương trình đường thẳng A B : y = a x + b , từ đó ta tìm được a = − 8 ; b = 5 . Vậy A B : y = − 8 x + 5 . Có điểm N 0 ; 5 thuộc đường thẳng này.

TXĐ: D = ℝ .
Ta có:
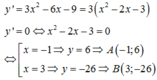
Phương trình đường thẳng đi qua hai điểm A và B là:
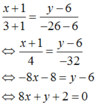
Dựa vào các đáp án ta có . N 1 , - 10 ∈ A B
Chọn D.
Đáp án A.
Ta có: D = R và y’ = 3x2 – 6x – 9, y’’ = 6x – 6.
Do đó y’ = 0 ⇔ x = -1 ∨ x = 3.
Do y’’(-1) = -12 < 0 và y’’(3) = 12 > 0 nên hàm số đạt cực tiểu tại x = 3.
Đồ thị hàm số y = x3 – 3x2 – 9x – 5 có điểm cực tiểu là (3; 32)