Tìm a và b để: Đường thẳng ax – 8y = b đi qua điểm M(9; -6) và đi qua giao điểm của hai đường thẳng ( ): 2x + 5y = 17, ( ): 4x – 10y = 14.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ (d): ax-8y=b ⇒ (d): 8y = ax-b
Ta có: (d): 8y=ax-b đi qua M(9; -6)
⇒ thay \(\left\{{}\begin{matrix}x=9\\y=-6\end{matrix}\right.\) vào 8y = ax-b, ta được:
8 *(-6) = 9a-b ⇔ - 48 = 9a-b (*)
+ (d1): 2x+5y=17 ⇒ (d1): 5y= -2x+17
(d2) : 2x-5y=7 ⇒ 5y=2x-7
Ta có phương trình hoành độ giao điểm của (d1) và (d2):
-2x+17 = 2x-7 ⇔ 4x=24 ⇔ x=6
⇒ y= 1
Gọi N là giao điểm của (d1) và (d2), ta có: N(6;1)
⇒ thay \(\left\{{}\begin{matrix}x=6\\y=1\end{matrix}\right.\) vào 8y = ax -b, ta được: 8= 6a-b (**)
Từ (*) và (**), ta có hpt:
\(\left\{{}\begin{matrix}-48=9a-b\\8=6a-b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-56\\b=6a-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{56}{3}\\b=-120\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=-\dfrac{56}{3}\\b=-120\end{matrix}\right.\)

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-5a+b=3\\\dfrac{3}{2}a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{8}{13}\\b=-\dfrac{1}{13}\end{matrix}\right.\)
b: Tọa độ giao điểm của (d1) và (d2) là;
\(\left\{{}\begin{matrix}2x+5y=17\\4x-10y=14\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=1\end{matrix}\right.\)
Vì (d3) đi qua M(9;-6) và N(6;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}6a-8=b\\9a+48=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6a-b=8\\9a-b=-48\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{56}{3}\\b=-120\end{matrix}\right.\)

Vì `(d') //// (d)=>{(a=a'=-1),(b ne b' ne 2):}`
Thay `a=-1;M(1;2)` vào `(d')` có: `2=-1+b<=>b=3` (t/m)
Do (d') song song với d nên \(a=-1\) ; \(b\ne2\)
\(\Rightarrow\) Phương trình (d'): \(y=-x+b\)
Do (d') đi qua M nên:
\(2=-1+b\Rightarrow b=3\)
Vậy \(\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\)

a: Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=5\\2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\)
b:
1: Thay x=-1 và y=3 vào (d), ta được:
\(2\cdot\left(-1\right)-a+1=3\)
=>-a-1=3
=>-a=4
hay a=-4

a: Thay x=-1 và y=-4 vào (d), ta được:
\(a\cdot\left(-1\right)+b=-4\)
=>-a+b=-4(1)
Thay x=2 và y=5 vào (d), ta được:
\(a\cdot2+b=5\)
=>2a+b=5(2)
Từ (1),(2) ta sẽ có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-4\\2a+b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=-9\\2a+b=5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=3\\b=5-2a=5-6=-1\end{matrix}\right.\)
Vậy: (d): y=3x-1
b: Để A,B,C thẳng hàng thì C nằm trên đường thẳng AB
=>C thuộc (d)
Thay x=m và y=8 vào y=3x-1, ta được:
3m-1=8
=>3m=9
=>m=3

Vì đường thẳng y = ax + b đi qua điểm ( 3;-5 )
=> -5 = 3a + b
Vì đường thẳng y = ax + b đi qua điểm ( -1 ; 3/2 )
=> 3/2 = -a + b
Giải hệ phương trình :
3a + b = -5
-a + b = 3/2
Ta có : 3a + b - ( -a + b ) = 3a + b + a - b = 4a = -5 - 3/2 = -13/2
=> a = -13/2 : 4 = -13/8
Thay a = -13/8 vào - a + b = 3/2 ta được :
13/8 + b = 3/2
=> b = 3/2 - 13/8 = -1/8
Vậy a = -13/8 ; b = -1/8
Vì đường thẳng y = ax + b đi qua điểm ( 3;-5 )
=> -5 = 3a + b
Vì đường thẳng y = ax + b đi qua điểm ( -1 ; 3/2 )
=> 3/2 = -a + b
Giải hệ phương trình :
3a + b = -5
-a + b = 3/2
Ta có : 3a + b - ( -a + b ) = 3a + b + a - b = 4a = -5 - 3/2 = -13/2
=> a = -13/2 : 4 = -13/8
Thay a = -13/8 vào - a + b = 3/2 ta được :
13/8 + b = 3/2
=> b = 3/2 - 13/8 = -1/8
Vậy a = -13/8 ; b = -1/8
Tọa độ giao điểm của hai đường thẳng ( d 1 ): 2x + 5y = 17, ( d 2 ): 4x – 10y = 14 là nghiệm của hệ phương trình: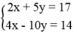
Khi đó ( d 1 ) và ( d 2 ) cắt nhau tại N(6; 1).
Đường thẳng ax – 8y = b đi qua điểm M(9; -6) và N(6;1) nên tọa độ của M và N nghiệm đúng phương trình đường thẳng.
*Điểm M: 9a + 48 = b
*Điểm N: 6a – 8 = b
Khi đó a và b là nghiệm của hệ phương trình: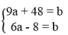
Vậy khi a = - 56/3 , b = -120 thì đường thẳng ax – 8y = b đi qua điểm M(9; -6) và đi qua giao điểm của hai đường thẳng ( d 1 ): 2x + 5y = 17, ( d 2 ): 4x – 10y = 14.