Biết rằng là các số thực thỏa mãn . Giá trị của bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Cách dựng:
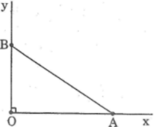
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 3 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
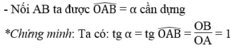

sin α = 0,25 = 14
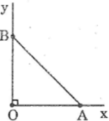
*Cách dựng: hình a
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 1 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
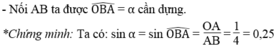
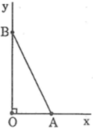

*Cách dựng: hình d
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 2 đơn vị dài
- Trên tia Oy dựng đoạn OB bằng 1 đơn vị dài

SABC=SADB+SADCSABC=SADB+SADC
<=>bc.sinA=AD⋅c⋅sinA2+AD⋅b⋅sinA2bc.sinA=AD⋅c⋅sinA2+AD⋅b⋅sinA2
<=>bc.sinA=AD⋅sinA2(b+c)bc.sinA=AD⋅sinA2(b+c)
<=>bc.sin2α=AD⋅sinα(b+c)bc.sin2α=AD⋅sinα(b+c)
<=>2b
a) Xét tam giác HAB và tam giác ABC có:
Góc AHB= góc BAC (= 900 )
B> là góc chung
⇒ tam giác HAB ~ tam giác ABC (g.g)
b) Xét ΔΔ ABC vuông tại A: BC2 = AB2 + AC2
Hay BC2 = 122 + 162
BC2 = 144 + 256 = 400
=> BC = √400 = 20 (cm)
Ta có : Δ HAB ∼ Δ ABC
=> HAAB=ABBCHAAB=ABBC
Hay HA12=1220HA12=1220
=> AH = 12.1220=7,212.1220=7,2 cm
c)
Ta có
DE là tia phân giác của góc ADB trong tam giác DAB,
áp dụng t/c tia phân giác thìDADB=AEEBDADB=AEEB
DG là tia phân giác cảu góc CDA trong tam giác CDA.
áp dụng t/c tia phân giác thì CDDA=CFFACDDA=CFFA
VẬy EAEB.DB

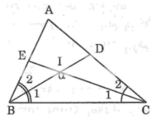
Trong ΔBIC có: ∠(BIC) + ∠B1 + ∠C1 = 180o (tổng 3 góc trong tam giác)
Suy ra: ∠B1 + ∠C1 = 180o - ∠(BIC)
Ta có:
∠B1 = 1/2 ∠B (vì BD là tia phân giác)
∠C1 = 1/2 ∠C (vì CE là tia phân giác)
Suy ra: ∠B + ∠C = 2(∠B1 + ∠C1) = 2.(180o - ∠(BIC))
Trong ΔABC có: ∠A + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Suy ra: ∠A = 180o - (∠B + ∠C) = 180o - 2.(180o - ∠(BIC)) = 2. ∠(BIC) – 180o
∠(BIC) = α thì ∠A = 2.α – 180o.
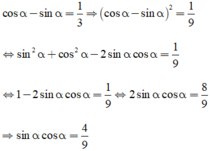
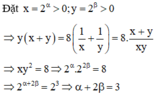
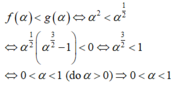
Chọn D.