mong mọi người giúp ạ :Tính chiều cao CH của tháp ở bên kia sông biết AB = 25cm; 0 0 43 ˆ 32 ; ˆ HAC = HBC = và ba điểm A, B, H thẳng hàng. (kết quả làm tròn đến chữ số thập phân thứ nhất)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều cao tháp và bóng lúc tia sáng hợp với mặt đất góc 24 độ là x, y thì ta có hệ
\(\hept{\begin{cases}x=y.tan24^o\\x=\left(y+8,5\right).tan20^o\end{cases}}\)

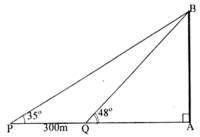
Ta có: A1B1 = AB = 12 m
Xét ΔDC1A1 có: C1A1 = C1D.cot49o
Xét ΔDC1B1 có: C1B1 = C1D.cot35o
Mà A1B1 = C1B1 - C1A1 = C1D.cot35o - C1D.cot49o
= C1D.(cot35o - cot49o)
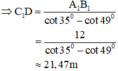
⇒ CD = CC1 + C1D = 1,3 + 21,47 = 22,77 m.
Vậy chiều cao của tháp là 22,77m.

Mỗi lần đi qua bên kia sông thì trên đò phải có 1 người và 1 quỷ. Tức là 1 người đi sang sông thì chở theo 1 quỷ đi.

Xét tam giác ADC có:
\(\widehat{ACB}=\widehat{ADC}+\widehat{DAC}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{DAC}=\widehat{ACB}-\widehat{ACB}=60^0-30^0=30^0\)
\(\Rightarrow\widehat{DAC}=\widehat{ADC}=30^0\)
=> Tam giác ADC cân tại C
=> AC=DC=20m
Áp dụng tslg trong tam giác ABC vuông tại B:
\(AB=sinC.AC=sin60^0.20=10\sqrt{3}\left(m\right)\)
\(BC=cosC.AC=cos60^0.20=10\left(m\right)\)