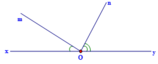
Cho góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy vẽ hai tia Om và On sao cho x O m ^ = 30 0 ; y O n ^ = 2 x O m ^ . Chứng tỏ Om vuông góc với On
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 2 2017
Om nằm giữa tia Oy và On
nÔm = mÔy = 1800 - 1200 = 600
=>xOm = xÔm - nÔm = 1200 - 600 = 600
Vậy a = 600
22 tháng 2 2017
Để Om nằm giữa Oy và On thì xOm < xOn
Mà xOm = 120o
Nên 180o < hoặc = xOn > 120o
26 tháng 7 2021
a) Vì là góc bẹt
⇒ Ox và Oy là 2 tia đối nhau
⇒ Tia On nằm giữa 2 tia Ox và Oy
Trên cùng 1 nửa mặt phẳng bờ xy, ta có:
⇒ Tia On nằm giữa 2 tia Ox và Om
+) Ta có: x O m ^ = 30 0 , y O n ^ = 2 x O m ^ = 2.30 0 = 60 0
Vì x O m ^ + m O y ^ = x O y ^ = 180 0 (hai góc kề bù)
=> m O y ^ = 180 0 − x O m ^ = 180 0 − 30 0 = 150 0
+) Xét trên nửa mặt phẳng có bờ chứa tia Oy, có : y O n ^ < y O m ^ (vì 0 ° < 60 ° < 150 ° )
=> Tia On nằm giữa hai tia Oy và Om
⇒ m O n ^ + n O y ^ = m O y ^ = 150 0 ⇒ m O n ^ + 60 0 = 150 0 ⇒ m O n ^ = 150 0 − 60 0 ⇒ m O n ^ = 90 0 ⇒ O m ⊥ O n .