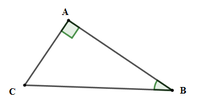
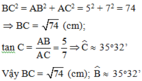Giải tam giác ABC có AB = 5cm, AC = 7cm ; \(\widehat{A}=42^0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2021
\(a,\widehat{C}=90^0-\widehat{B}=40^0\\ AB=\cos B\cdot BC\approx3,9\left(cm\right)\\ AC=\sin B\cdot BC\approx4,6\left(cm\right)\\ b,BC=\sqrt{AB^2+AC^2}=\sqrt{74}\left(cm\right)\\ \sin B=\dfrac{AC}{BC}=\dfrac{7\sqrt{74}}{74}\approx\sin54^0\\ \Rightarrow\widehat{B}\approx54^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx36^0\)
TT
5
14 tháng 3 2023
Xét ΔACB có AD là phân giác
nên BD/AB=CD/AC
=>CD/7=2/5
=>CD=2,8cm
8 tháng 2 2017
A B C D 5 7 H
Kẻ AH vuông góc BC.
Áp dụng định lý Pytago tính được BC = \(\sqrt{74}\)
Sử dụng TC đường PG trong tam giác; có :
\(\frac{BD}{AB}=\frac{CD}{AC}\)
\(\Rightarrow\frac{BD}{7}=\frac{DC}{5}=\frac{BD+DC}{7+5}=\frac{\sqrt{74}}{12}\)
Tìm được \(CD=\frac{5\sqrt{74}}{12}\)
Sử dụng diện tích tam giác để tìm ra \(AH=\frac{35\sqrt{74}}{74}\)
Dùng Pytago tìm ra CH = \(\frac{25\sqrt{74}}{74}\)
Suy ra HD = CD - CH = ...
Rồi sử dụng Pytago tính AD.
Kiểm tra lại đề.