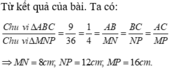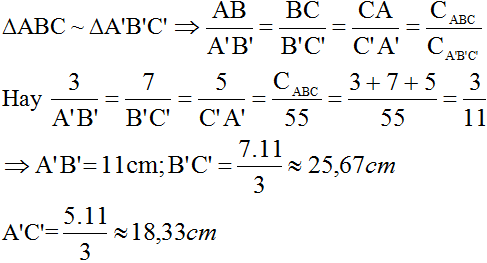Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MN}{5}=\dfrac{NP}{9}=\dfrac{MP}{7}=\dfrac{MN+NP+MP}{5+9+7}=\dfrac{5.25}{21}=0.25\)
Do đó: MN=1,25(cm); NP=2,25(cm); MP=1,75(cm)
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
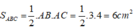
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
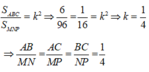
Thay số
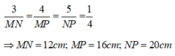
Chọn đáp án B
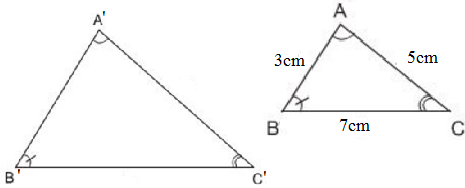
- PABC=AB+AC+BC=5+7+9=21cm.
- Vì △ABC∼△MNP nên:
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}=\dfrac{P_{ABC}}{P_{MNP}}=\dfrac{21}{5,25}=4\)
=>\(\left[{}\begin{matrix}MN=\dfrac{AB}{4}=\dfrac{5}{4}=1,25\left(cm\right)\\MP=\dfrac{AC}{4}=\dfrac{7}{4}=1,75\left(cm\right)\\NP=\dfrac{BC}{4}=\dfrac{9}{4}=2,25\left(cm\right)\end{matrix}\right.\)
Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’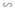 
ΔABC ⇒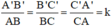 
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
∆ABC ∽ ∆A'B'C' => = = =
hay = = = =
=> A'B' = 11cm;
B'C' = ≈ 25.67 cm
A'C' = ≈ 18,33 cm
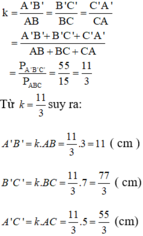
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)