Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho o là trung điểm của đoạn AB. Trên cùng môtj nửa mặt phẳng có bờ là cạnh AB vẽ tia Ax, By cùng vuông góc với Ab. TRên tia Ax lấy C( khác A), qua o kẻ đường thawnggr vuông góc với OC cắt By tại D.
a. CM: (AB)^2= 4AC.BD
minh se noi cach tu duy cua minh, mong ban hieu
AB^2=4AC.BD=>(2OA)^2=4AC.BD=>4OA^2=4AC.BD=>Ban phai chung minh OA^2=AC.BD
Day la cach chung minh: goc COA+COD+DOB=180
Ma COD=90(theo gt)=>COA+BOD=90(1)
Trong tam giac COA co CAO=90:COA+ACO=90(2)
Tu (1)va(2) ta=>BOD=ACO
xet tam giac CAO va OBD co:
CAO=OBD=90
BOD=ACO(theo cm tren)
=>tam giac CAO dong dang voi tam giac OBD=>AC/OA=OB/BD=>AC/OA=OA/BD=>OA^2=AC.BD
a: Gọi giao điểm của CO với BD là K
Xét ΔOAC vuông tại A và ΔOBK vuông tại B có
OA=OB
\(\widehat{AOC}=\widehat{BOK}\)
Do đó: ΔOAC=ΔOBK
=>OC=OK và \(\widehat{ACO}=\widehat{BKO}\)
=>\(\widehat{ACO}=\widehat{DKC}\)(1)
OC=OK
K,O,C thẳng hàng
Do đó: O là trung điểm của KC
Xét ΔDCK có
DO là đường cao
DO là đường trung tuyến
Do đó: ΔDCK cân tại D
=>\(\widehat{DCK}=\widehat{DKC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{ACO}=\widehat{HCO}\)
Xét ΔCAO vuông tại A và ΔCHO vuông tại H có
CO chung
\(\widehat{ACO}=\widehat{HCO}\)
Do đó: ΔCAO=ΔCHO
=>OA=OH=R
=>H thuộc (O)
b: Xét (O) có
OH là bán kính
CD\(\perp\)OH tại H
Do đó: CD là tiếp tuyến của (O)
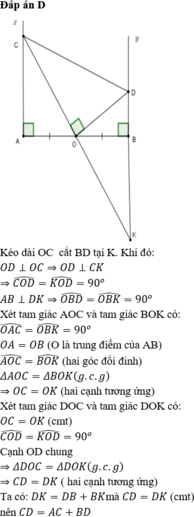
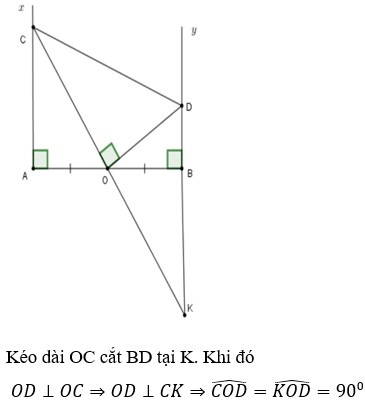
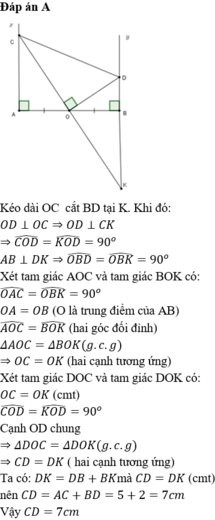
a)
Ta có:
\(AC.BD=\dfrac{AB^2}{4}=\dfrac{AB}{2}.\dfrac{AB}{2}=AO.OB\Leftrightarrow\dfrac{AC}{AO}=\dfrac{OB}{BD}\)
Xét 2 tam giác BOD và COD có:\(\dfrac{AC}{AO}=\dfrac{OB}{BD};\widehat{A}=\widehat{B}=90\)
nên tam giác BOD đồng dạng với tam giác ACO nên:
\(\widehat{AOC}=\widehat{ODB}\) mà \(\widehat{ODB}+\widehat{DOB}=90\Leftrightarrow\widehat{AOC}+\widehat{DOB}=90\)
Lại c:\(\widehat{COD}+\widehat{AOC}+\widehat{BOD}=180\Leftrightarrow\widehat{COD}=90\)
Hay tam giác COD vuông tại O(ĐPCM)
b)Xét tam giác ACO và tam giác BOD đồng dạng nên:
\(\dfrac{BD}{AO}=\dfrac{OD}{OC}\Leftrightarrow\dfrac{BD}{OB}=\dfrac{OD}{OC}\)
Xét tam giác BOD và tam giác COD có:\(\dfrac{BD}{OB}=\dfrac{OD}{OC};\widehat{COD}=\widehat{B}=90\)
nên tam giác BOD đồng dạng với tam giác COD (ĐPCM)
quên không bảo bạn tự vẽ hình nha