Câu 11. Cho tứ diện ABCD có AB = AC = AD = BD = a và \(\widehat{BAC}=\text{120°};\widehat{CAD}=\text{90°}\) . Góc giữa \(\overrightarrow{AB}\&\overrightarrow{CD}\)
A. \(\text{120°}\) B. \(\text{180°}\) C. \(\text{90°}\) D.\(\text{45°}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(S_{\Delta ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{a^2\sqrt{3}}{4}\)
\(V=\dfrac{AB.AC.AD}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{a^3\sqrt{2}}{12}\)
\(\Rightarrow d\left(B;\left(ACD\right)\right)=\dfrac{3V}{S}=\dfrac{a\sqrt{6}}{3}\)
CM
8 tháng 12 2017
Đáp án D
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
CM
25 tháng 3 2018
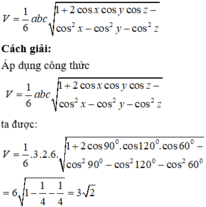
Ta có:
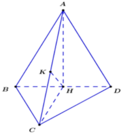
Xét ∆ A H C vuông tại H có đường cao KH ta có:
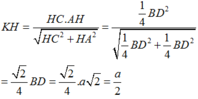
Chọn B.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) \(\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC \Rightarrow d\left( {C,AB} \right) = BC = b\).
b)
\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC\\\widehat {ABD} = {90^ \circ } \Rightarrow AB \bot BD\end{array} \right\} \Rightarrow AB \bot \left( {BC{\rm{D}}} \right)\\\left. \begin{array}{l} \Rightarrow AB \bot C{\rm{D}}\\\widehat {BC{\rm{D}}} = {90^ \circ } \Rightarrow BC \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABC} \right)\\ \Rightarrow d\left( {D,\left( {ABC} \right)} \right) = C{\rm{D}} = \sqrt {B{{\rm{D}}^2} - B{C^2}} = \sqrt {{c^2} - {b^2}} \end{array}\)
c) \(AB \bot BC,C{\rm{D}} \bot BC \Rightarrow d\left( {AB,C{\rm{D}}} \right) = BC = b\).
\(CD=\sqrt{AC^2+AD^2}=a\sqrt{2}\)
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cos\widehat{BAC}}=a\sqrt{3}\)
\(\Rightarrow BD^2+CD^2=BC^2\Rightarrow CD\perp BD\)
\(cos\widehat{ADC}=\frac{AD}{CD}=\frac{1}{\sqrt{2}}\)
\(cos\left(\overrightarrow{AB};\overrightarrow{CD}\right)=\frac{\overrightarrow{AB}.\overrightarrow{CD}}{AB.CD}=\frac{\left(\overrightarrow{AD}+\overrightarrow{DB}\right).\overrightarrow{CD}}{a^2\sqrt{2}}=\frac{\overrightarrow{AD}.\overrightarrow{CD}}{a^2\sqrt{2}}=\frac{a.a\sqrt{2}.\frac{1}{\sqrt{2}}}{a^2\sqrt{2}}=\frac{1}{\sqrt{2}}\)
\(\Rightarrow\left(\overrightarrow{AB};\overrightarrow{CD}\right)=45^0\)
Vẽ hình? :)