Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
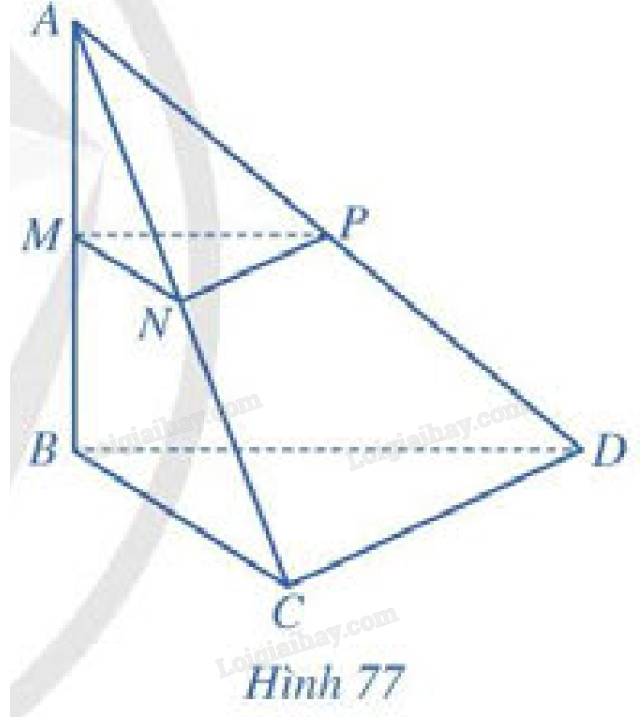
Do \(AB=AC\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow AM\) là trung tuyến đồng thời là đường cao
\(\Rightarrow AM\perp BC\) (1)
Mà \(\left\{{}\begin{matrix}AD\perp AB\left(gt\right)\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABC\right)\Rightarrow AD\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(ADM\right)\)
b.
Từ A kẻ \(AE\perp DM\) (E thuộc DM)
Do \(BC\perp\left(ADM\right)\Rightarrow BC\perp AE\)
\(\Rightarrow AE\perp\left(BCD\right)\Rightarrow AE=d\left(A;\left(BCD\right)\right)\)
\(BC=\sqrt{AB^2+AC^2}=5\sqrt{2}\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông ADM:
\(AE=\dfrac{AD.AM}{\sqrt{AD^2+AM^2}}=\dfrac{5\sqrt{3}}{3}\)
c.
Do \(AD\perp\left(ABC\right)\) theo cmt \(\Rightarrow AM\) là hình chiếu vuông góc của DM lên (ABC)
\(\Rightarrow\widehat{DMA}\) là góc giữa DM và (ABC)
\(tan\widehat{DMA}=\dfrac{AD}{AM}=\sqrt{2}\Rightarrow\widehat{DMA}\approx54^044'\)


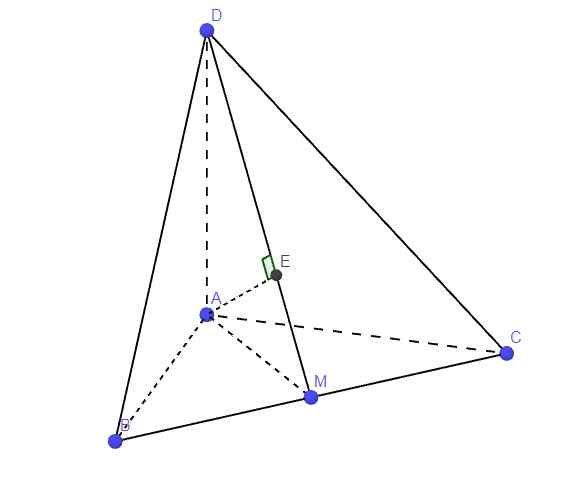
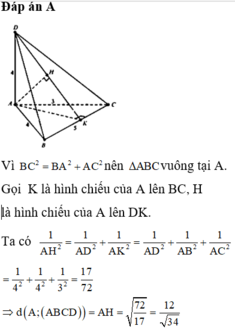
Dựng CH _|_ AB => CH _|_ (SAB)
Giả sử MN cắt AD tại F. Theo định lý Talet ta có:
\(\frac{DF}{MC}=\frac{ND}{NC}=\frac{1}{2}\Rightarrow DF=\frac{MC}{2}=\frac{a}{4}\)
Khi đó \(\frac{PA}{PC}=\frac{AF}{MC}=\frac{5}{2}\Rightarrow\frac{CA}{PA}=\frac{7}{5}\)
Do đó: d (P;(SAB))=\(\frac{5}{7}d\left(C;\left(SAB\right)\right)=\frac{5}{7}CH=\frac{5}{7}\cdot\frac{a\sqrt{3}}{2}=\frac{5a\sqrt{3}}{14}\)

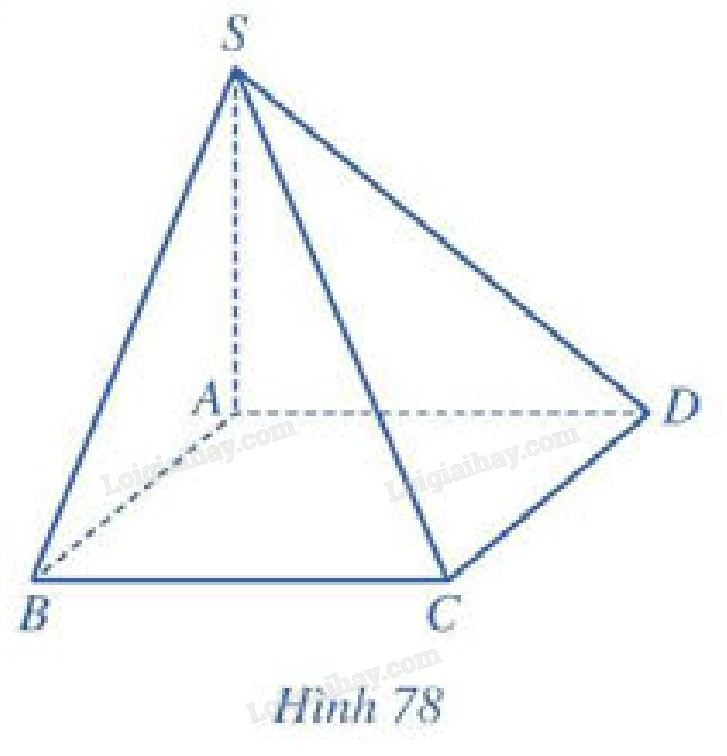
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).


Kẻ \(OI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right),OH \bot SI\left( {H \in SI} \right)\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot C{\rm{D}}\\OI \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SOI} \right)\\\left. \begin{array}{l} \Rightarrow C{\rm{D}} \bot OH\\OH \bot SI\end{array} \right\} \Rightarrow OH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {O,\left( {SC{\rm{D}}} \right)} \right) = OH\end{array}\)
\(\Delta ABC\) đều \( \Rightarrow AC = a \Rightarrow OC = \frac{1}{2}AC = \frac{a}{2}\)
\(\Delta ABD\) có \(\widehat {BA{\rm{D}}} = {120^ \circ } \Rightarrow B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2} - 2{\rm{A}}B.A{\rm{D}}} = a\sqrt 3 \Rightarrow OD = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta OCD\) vuông tại \(O\) có đường cao \(OI\)
\( \Rightarrow OI = \frac{{OC.O{\rm{D}}}}{{C{\rm{D}}}} = \frac{{a\sqrt 3 }}{4}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI \Rightarrow \Delta SOI\) vuông tại \(O\) có đường cao \(OH\)
\( \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {51} }}{{17}}\)
Vậy \(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{{a\sqrt {51} }}{{17}}\).

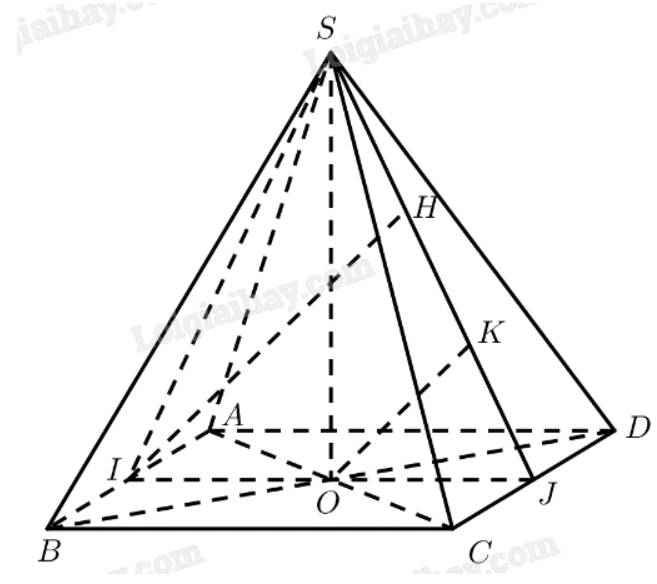
a) Gọi \(O\) là tâm của đáy
\( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AB\)
\(I\) là trung điểm của \(AB\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow IJ\) là đường trung bình của hình vuông \(ABCD\)
\(\left. \begin{array}{l} \Rightarrow IJ\parallel A{\rm{D}}\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow IJ \bot AB\)
Ta có:
\(\left. \begin{array}{l}SO \bot AB\\IJ \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {SIJ} \right)\)
b) Kẻ \(IH \bot SJ\left( {H \in SJ} \right),OK \bot SJ\left( {K \in SJ} \right) \Rightarrow IH\parallel OK\)
\(O\) là trung điểm của \(IJ \Rightarrow IH = 2{\rm{O}}K\)
Ta có:
\(\left. \begin{array}{l}AB\parallel C{\rm{D}}\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {AB,SC} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}\left. \begin{array}{l}AB \bot \left( {SIJ} \right)\\C{\rm{D}}\parallel AB\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SIJ} \right) \Rightarrow C{\rm{D}} \bot IH\\ & IH \bot SJ\end{array} \right\} \Rightarrow IH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {AB,C{\rm{D}}} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right) = IH\end{array}\)
\(O\) là trung điểm của \(IJ\), \(IH\parallel {\rm{O}}K\)\( \Rightarrow IH = 2{\rm{O}}K\)
\(O\) là trung điểm của \(B{\rm{D}}\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow OJ\) là đường trung bình của \(\Delta BCD\)
\( \Rightarrow OJ = \frac{1}{2}BC = \frac{a}{2}\)
\(\Delta ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SAO\) vuông tại \(O\)\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \frac{{a\sqrt 6 }}{2}\)
\(\Delta SOJ\) vuông tại \(O\) có đường cao \(OK\)
\( \Rightarrow OK = \frac{{SO.OJ}}{{\sqrt {S{O^2} + O{J^2}} }} = \frac{{a\sqrt {42} }}{{14}}\)
\( \Rightarrow d\left( {AB,C{\rm{D}}} \right) = IH = 2OK = \frac{{a\sqrt {42} }}{7}\)

Chọn A
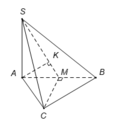
Xác định được
![]()
![]()
Do M là trung điểm của cạnh AB nên
![]()
![]()
![]()
Tam giác vuông SAM có
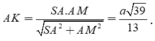
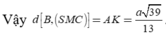
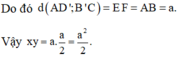
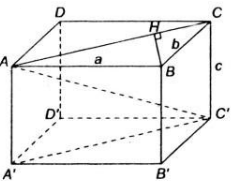

a) \(\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC \Rightarrow d\left( {C,AB} \right) = BC = b\).
b)
\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC\\\widehat {ABD} = {90^ \circ } \Rightarrow AB \bot BD\end{array} \right\} \Rightarrow AB \bot \left( {BC{\rm{D}}} \right)\\\left. \begin{array}{l} \Rightarrow AB \bot C{\rm{D}}\\\widehat {BC{\rm{D}}} = {90^ \circ } \Rightarrow BC \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABC} \right)\\ \Rightarrow d\left( {D,\left( {ABC} \right)} \right) = C{\rm{D}} = \sqrt {B{{\rm{D}}^2} - B{C^2}} = \sqrt {{c^2} - {b^2}} \end{array}\)
c) \(AB \bot BC,C{\rm{D}} \bot BC \Rightarrow d\left( {AB,C{\rm{D}}} \right) = BC = b\).