Cho \(\Delta ABC;\widehat{A}=2\widehat{B},AC=9,BC=12.\) Tính AB?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét \(\Delta ACB\) và \(\Delta EDF\) có:
\(\begin{array}{l}AC = ED\\AB = EF\\CB = DF\end{array}\)
\(\Rightarrow \Delta ACB = \Delta EDF\)(c.c.c)
Xét \(\Delta CAB\) và \(\Delta DEF\) có:
\(\begin{array}{l}CA = DE\\AB = EF\\CB = DF\end{array}\)
\(\Rightarrow \Delta CAB = \Delta DEF\)(c.c.c)
Vậy khẳng định (2) và (4) đúng.
Chú ý: Khi \(\Delta ABC = \Delta DEF\), ta cũng có thể viết \(\Delta BAC = \Delta EDF\) hay \(\Delta CBA = \Delta FED\);....
25 tháng 3 2023
a)xét ΔABC và ΔHBA ta có
\(\widehat{BAH}=\widehat{BHA}=90^o\)
\(\widehat{B}chung\)
=>ΔABC ∼ ΔHBA(g.g)(1)
b)xét ΔABC và ΔAHC ta có
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{B}chung\)
->ΔABC ∼ ΔAHC(g.g)(2)
từ (1) và (2)=>ΔHBA và ΔAHC
->\(\dfrac{AH}{BH}=\dfrac{HC}{AH}\)
=>\(AH^2=BH.HC\)
3 tháng 3 2023
a: Xét ΔAMB vuông tại M và ΔANC vuông tạiN có
góc A chung
=>ΔAMB đồng dạng vơi ΔANC
=>AM/AN=AB/AC
=>AM*AC=AB*AN; AM/AB=AN/AC
b: Xét ΔAMN và ΔABC có
AM/AB=AN/AC
góc A chung
=>ΔAMN đồng dạng với ΔABC
=>góc AMN=góc ABC
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
Khẳng định d) là khẳng định không đúng
=> ΔACB \(\backsim\) ΔMPN
26 tháng 6 2022
Bài 2:
Ta có: AM=1/2BC
nên AM=BM=CM
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
=>\(\widehat{MAB}=\widehat{B}\)
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{C}\)
Xét ΔBAC có \(\widehat{BAC}+\widehat{B}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{MAB}+\widehat{B}+\widehat{MAC}+\widehat{C}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)=180^0\)
=>\(\widehat{BAC}=90^0\)
hay ΔABC vuông tại A
10 tháng 5 2023
Gọi M là trung điểm của BC, D là chân đường phân giác kẻ từ A xuống BC
=>A,G,M thẳng hàng và A,I,D thẳng hàng
BM=CM=BC/2=7,5cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/4=CD/6=15/10=1,5
=>BD=6cm
=>MD=1,5cm
IG//DM
=>IG/DM=AI/AD=2/3
=>IG=2/3DM=1cm
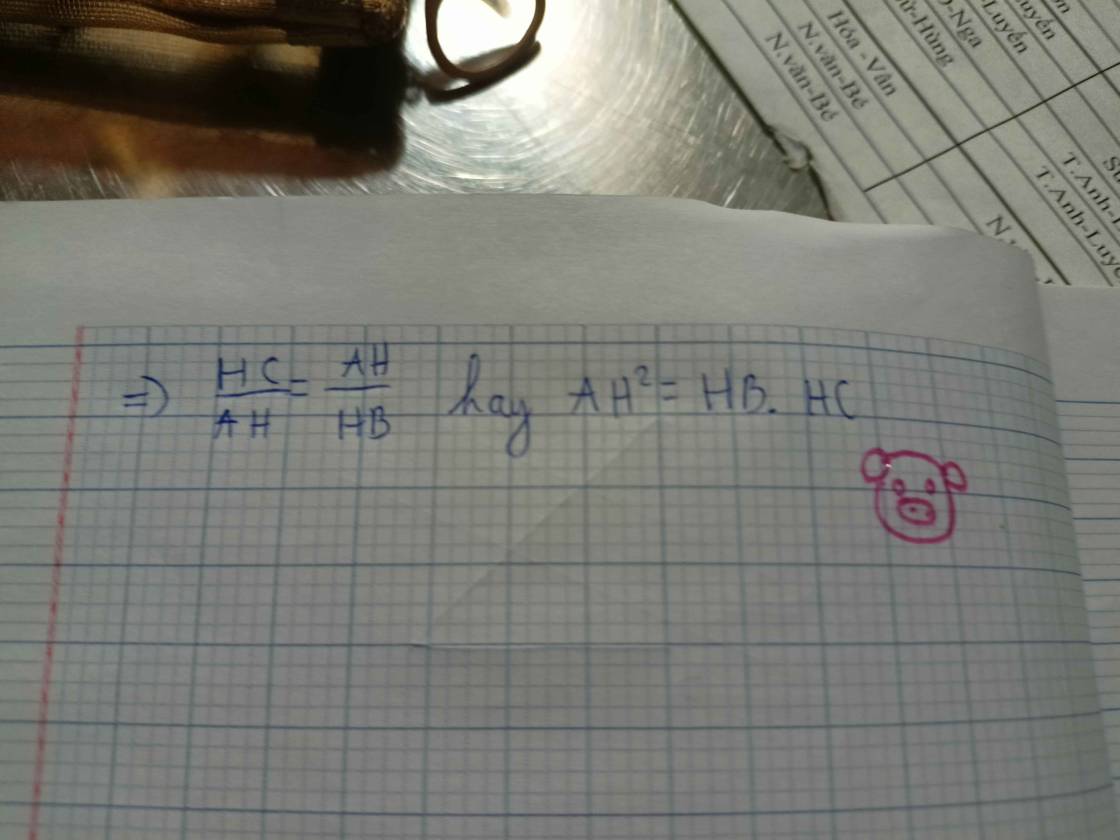
Kẻ phân giác AD (D thuộc BC)
\(\Rightarrow\widehat{B}=\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{A}}{2}\)
Xét hai tam giác ABC và DAC có:
\(\left\{{}\begin{matrix}\widehat{C}\text{ chung}\\\widehat{B}=\widehat{CAD}\end{matrix}\right.\) \(\Rightarrow\Delta ABC\sim\Delta DAC\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{DC}=\dfrac{BC}{AC}\Rightarrow DC=\dfrac{AC^2}{BC}=\dfrac{27}{4}\)
\(\Rightarrow BD=BC-DC=\dfrac{21}{4}\)
Áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{DC}{AC}\Rightarrow AB=\dfrac{BD.AC}{DC}=7\)