cho hàm số (P): y=ax2
a) tìm hệ số a biết đồ thị (P) đi qua điểm A \(\left(\dfrac{-1}{2};\dfrac{-1}{4}\right)\)
b) viết pt đường thẳng (d), biết đồ thị (d) song song với đường thẳng y=-2x-1 và tiếp xúc với (P)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, y = ax^2 đi qua B(2;4)
<=> 4a = 4 <=> a = 1
b, bạn tự vẽ
a: Thay x=2 và y=4 vào hàm số, ta được:
\(a\cdot4=4\)
hay a=1
b: Thay x=2 và y=4 vào hàm số, ta được:
4a=4
hay a=1

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 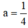
Vậy hàm số: 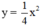
| x | -4 | -2 | 0 | 2 | 4 |
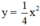 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
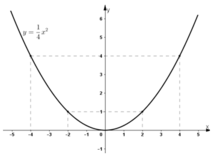

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 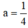
Vậy hàm số: 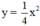
| x | -4 | -2 | 0 | 2 | 4 |
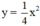 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
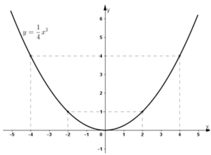

Lời giải:
a) Vì ĐTHS đi qua điểm $A$ nên:
$y_A=ax_A^2$
$\Leftrightarrow -1=a.2^2\Rightarrow a=-\frac{1}{4}$
b) Vậy hàm số có công thức: $y=\frac{-1}{4}x^2$
Hình vẽ:

1) Để (P) đi qua điểm A(1;-2) thì
Thay x=1 và y=-2 vào hàm số \(y=ax^2\), ta được:
\(a\cdot1^2=-2\)
hay a=-2

a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
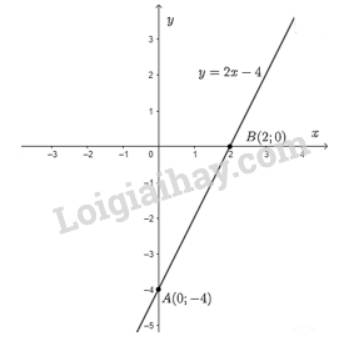
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).

a) Thay x=1 và y=2 vào (P), ta được:
\(a\cdot1^2=2\)
hay a=2
Vì đồ thị (p) đi qua điểm \(A\left(\dfrac{-1}{2};\dfrac{-1}{4}\right)\) nên ta có:
\(-\dfrac{1}{4}=a.\left(-\dfrac{1}{2}\right)^2\)
\(\Rightarrow-\dfrac{1}{4}=a.\dfrac{1}{4}\Rightarrow a=-1\)
Khi đó hàm số (p) có dạng: \(y=-x^2\)
Gọi phương trình đường thẳng (d) cần tìm là: \(y=ax+b\left(a\ne0\right)\)
Vì (d) song song với đường thẳng \(y=-2x-1\)
\(\Rightarrow\left\{{}\begin{matrix}a=-2\\b\ne-1\end{matrix}\right.\)
Phương trình (d) có dạng \(y=-2x+b\left(b\ne-1\right)\)
Xét phương trình hoành độ tiếp điểm của (p) và (d) :
\(-x^2=-2x+b\)
\(\Leftrightarrow-x^2+2x-b=0\left(1\right)\)
Xét phương trình (1) có \(\Delta=2^2-4.\left(-1\right).\left(-b\right)=4-4b\)
Vì (d) tiếp xúc với (p) \(\Rightarrow\) phương trình (1) có nghiệm kép \(\Leftrightarrow\Delta=0\Leftrightarrow4-4b=0\Leftrightarrow b=1\) (tm \(b\ne-1\) )
Vậy phương trình đường thẳng (d) cần tìm là \(y=-2x+1\)
Vì Parabol (P) đi qua điểm \(A\left(\dfrac{-1}{2};-\dfrac{1}{4}\right)\) nên thỏa mãn:
\(a.\left(-\dfrac{1}{2}\right)^2=-\dfrac{1}{4}\\ \Leftrightarrow a.\dfrac{1}{4}=-\dfrac{1}{4}\\ \Leftrightarrow a=-1\)
Vậy hệ số a của (P) là -1
b,Giả sử pt đường thẳng (d) có dạng y=ax+b
Vì (d) song song với đường thẳng y=-2x-1 nên thỏa mãn:
\(\left\{{}\begin{matrix}a=-2\\b\ne-1\end{matrix}\right.\)
Khi đó phương trình đường thẳng (d) trở thành y=-2x+b
Ta có phương trình hoành độ giao điểm của (d) và (P) là
\(-x^2+2x-b=0\) (*)
Vì pt đường thẳng (d) tiếp xúc với (P) nên phương trình (*) có 1 nghiệm duy nhất tức là \(\Delta\)'=0\(\Leftrightarrow1^2-b=0\\ \Leftrightarrow b=1\left(tmđk\right)\)
Vậy phương trình đường thẳng (d) là y=-2x+1