\(\left(3x-2\right)\) chia hết \(2x+1\)

\(2\left(3x-2\right)\) chia hết \(\left(2x+1\right)\)

\(6x-4\) chia hết \(2x+1\)

\(3\left(2x+1\right)-7\) chia hết \(2x+1\)

7 chia hết \(2x+1\)

\(2x+1\inƯ\left(7\right)\)

\(2x+1\in\left\{-7;-1;1;7\right\}\)

\(x\in\left\{-4;-1;0;3\right\}\)

mik cảm ơn

\(2^{x+2}-2^x=96\)

\(2^x.\left(2^2-1\right)=96\)

\(2^x.3=96\)

\(2^x=96:3\)

\(2^x=32\)

\(2^x=2^5\)

\(x=5\)

Tổng số bánh của 10 gói bánh là: 

`10 xx 36 = 360` (cái bánh) 

Số bánh mà các bạn ăn là: 

`360 xx 3/4 = 270` (cái)

Số bánh còn lại là: 

`360 - 270 = 90` (cái)

Mỗi bạn được chia số bánh là: 

`90 : 10 = 9` (cái)

Đáp số: ...

Tổng số cái bánh trong 10 gói bánh là:

                     36x10=360 (cái)

Số cái bánh các bạn đã ăn hết là:

                     360x\(\dfrac{3}{4}\) = 270( cái)

Số cái bánh còn lại là:

                     360-270=90 (cái)

Mỗi bạn có số cái bánh là:

                     90:10= 9 (cái)

                             Đáp số: 9 cái

Bao nhiêu chữ số vậy bạn?

\(\dfrac{2^{32}.5^{24}}{5^{23}.2^{35}}=\dfrac{5^{24}}{5^{23}}.\dfrac{2^{32}}{2^{35}}=\dfrac{5^1}{2^3}=\dfrac{5}{8}\)

\(\dfrac{10^{15}.9^8.4^7}{20^{14}.3^{18}}=\dfrac{\left(2.5\right)^{15}.\left(3^2\right)^8.\left(2^2\right)^7}{\left(2^2.5\right)^{14}.3^{18}}=\dfrac{2^{15}.5^{15}.3^{16}.2^{14}}{2^{28}.5^{14}.3^{18}}=\dfrac{2^{29}.3^{16}.5^{15}}{2^{28}.3^{18}.5^{14}}=\dfrac{2.5}{3^2}=\dfrac{10}{9}\)

\(\dfrac{27^5.25^7}{125^5.9^8}=\dfrac{\left(3^3\right)^5.\left(5^2\right)^7}{\left(5^3\right)^5.\left(3^2\right)^8}=\dfrac{3^{15}.5^{14}}{5^{15}.3^{16}}=\dfrac{1}{5.3}=\dfrac{1}{15}\)

\(\dfrac{\left(-2\right)^{12}.9^4}{\left(-3\right)^9.16^2}=\dfrac{\left(-1.2\right)^{12}.\left(3^2\right)^4}{\left(-1.3\right)^9.\left(2^4\right)^2}=\dfrac{\left(-1\right)^{12}.2^{12}.3^8}{\left(-1\right)^9.3^9.2^8}=\dfrac{1.2^{12}.3^8}{\left(-1\right).2^8.3^9}=\dfrac{2^4}{\left(-1\right).3}=-\dfrac{8}{3}\)

bó tay

110 độ

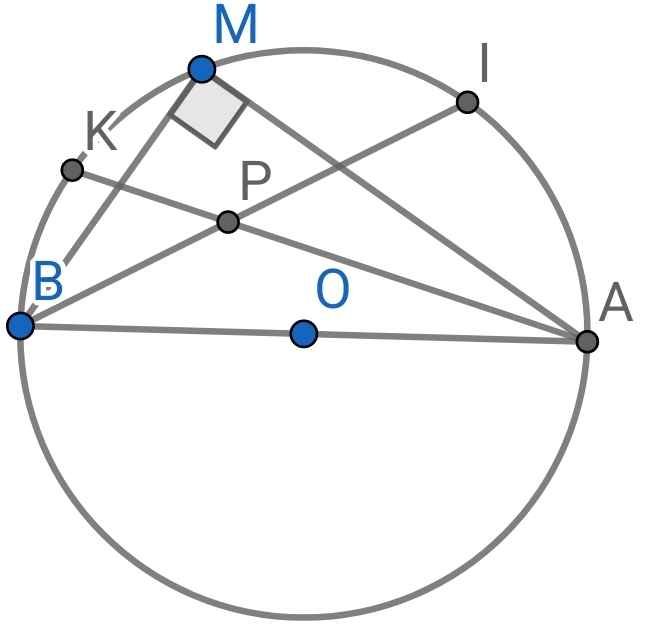
a) Do MA ⊥ MB (gt)

⇒ ∠MAB = 90⁰

⇒ M, A, B thuộc đường tròn đường kính AB

Mà M, A, B thuộc (O)

⇒ O là trung điểm của AB

⇒ A, O, B thẳng hàng

b) Do I là điểm chính giữa của cung nhỏ MA (gt)

⇒ sđ cung AI = sđ cung MI

⇒ ∠ABI = ∠MBI (hai góc nội tiếp chắn hai cung bằng nhau)

⇒ BI là tia phân giác của ∠ABM

Do K là điểm chính giữa của cung MB (gt)

⇒ sđ cung BK = sđ cung MK

⇒ ∠BAK = ∠MAK (hai góc nội tiếp chắn hai cung bằng nhau)

⇒ AK là tia phân giác của ∠BAM

Mà P là giao điểm của AK và BI (gt)

⇒ P là giao điểm của ba đường phân giác của ∆MAB

⇒ P là tâm đường tròn nội tiếp ∆MAB

a.

Do \(OM=OA=R\Rightarrow\Delta OAM\) cân tại O

\(\Rightarrow\widehat{OAM}=\widehat{OMA}\Rightarrow\widehat{AOM}=180^0-\left(\widehat{OAM}+\widehat{OMA}\right)=180^0-2\widehat{OMA}\)

Tương tự, \(\Delta OBM\) cân tại O

\(\Rightarrow\widehat{BOM}=180^0-2\widehat{OMB}\)

\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2\left(\widehat{OMA}+\widehat{OMB}\right)\)

\(\Rightarrow\widehat{AOM}+\widehat{BOM}=360^0-2.\widehat{AMB}=360^0-2.90^0=180^0\)

\(\Rightarrow A,O,B\) thẳng hàng

b.

Do I là điểm chính giữa cung MA \(\Rightarrow sđ\stackrel\frown{AI}=sđ\stackrel\frown{MI}\Rightarrow\widehat{ABI}=\widehat{MBI}\)

\(\Rightarrow BI\) là tia phân giác góc \(\widehat{ABM}\) (1)

Do K là điểm chính giữa cung MB \(\Rightarrow sđ\stackrel\frown{MK}=sđ\stackrel\frown{BK}\Rightarrow\widehat{MAK}=\widehat{BAK}\)

\(\Rightarrow AK\) là tia phân giác góc \(\widehat{MAB}\) (2)

(1);(2) \(\Rightarrow P\) là giao điểm 2 đường phân giác trong của tam giác MAB

\(\Rightarrow P\) là tâm đường tròn nội tiếp tam giác MAB

        Olm chào em đây là dạng toán nâng cao chuyên đề sự tăng giảm diện tích lồng hiệu tỉ, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này băng các kết hợp nhiều phương pháp (dựng hình phụ kết hợp hiệu tỉ ẩn tỉ) như sau:

                                        Giải:

a; Theo bài ra ta có hình minh họa h1.

Mảnh ban đầu là ABCD. Mảnh đất lúc sau là AEFG. 

JI = JB nên JI bẳng chiều rộng lúc sau. Diện tích DHIG là diện tích bị  giảm.

Từ những lập luận trên ta có:  Hiệu của chiều dài lúc đầu và chiều rộng lúc sau là:

           525 :   5 = 105 (m)

Hiệu của chiều dài lúc đầu và chiều rộng lúc dầu là: 

          105 - 5  = 100 (m)

Theo bài ra ta có sơ đồ:

Theo sơ đồ ta có:

Chiều dài lúc đầu của hình chữ nhật là: 100 :( 5 - 1 ) x 5 = 125 (m)

Chiều rộng lúc đầu của hình chữ nhật là: 125 : 5 = 25 (m)

Diện tích ban đầu của hình chữ nhật là: 

          125 x 25 = 3125 (m²)

b; Cả mảnh đất thu được số ki-lô-gam đậu là:

         80 x 3125 : 100 = 2500(kg)

           2500 kg = 25 tạ 

Đáp số: a; 3125 m²

              b; 25 tạ.

Gọi số xe to hoặc số xe nhỏ lần lượt là \(a,b\)(xe) (\(a,b\inℕ^∗\)) 

Theo bài ra, ta có hệ phương trình: 

\(\hept{\begin{cases}a=b-2\\\frac{180}{a}-\frac{180}{b}=15\end{cases}}\Leftrightarrow\hept{\begin{cases}a=b-2\\\frac{180}{b-2}-\frac{180}{b}=15\end{cases}\Leftrightarrow\hept{\begin{cases}a=b-2\\\frac{360}{b\left(b-2\right)}=15\end{cases}}}\)

\(\frac{360}{b\left(b-2\right)}=15\Rightarrow15b\left(b-2\right)=360\Leftrightarrow\orbr{\begin{cases}b=6\left(tm\right)\\b=-4\left(l\right)\end{cases}}\)

Suy ra \(\hept{\begin{cases}a=4\\b=6\end{cases}}\). 

số xe to là 4

số xe nhỏ là 6