Lời giải:

$A=a^3+b^3+c^3-3abc=(a^3+b^3)-3abc+c^3$

$=(a+b)^3-3ab(a+b)-3abc+c^3$

$=[(a+b)^3+c^3]-[3ab(a+b)+3abc]$

$=(a+b+c)[(a+b)^2-(a+b)c+c^2]-3ab(a+b+c)$

$=(a+b+c)[(a+b)^2-(a+b)c+c^2-2ab]$

$=(a+b+c)(a^2+b^2+c^2-ab-bc-ac)$

Bạn xem lại câu A nhé dãy A toàn các số hạng chia hết cho 3 mà số cuối 2023 lại không chia hết cho 3, dãy A không tuân theo quy luật nào cả không thể tính được bạn nhé

H = 2012.3+2012.4+...+2012.2011

= 2012.(3+4+...+2011)

Xét riêng: B=3+4+...+2011

Số số hạng dãy trên:

  (2011-3):1+1=2009 (số hạng)

Tổng dãy B là:

  (2011+3).2009:2=2023063

Do vậy: H = 2012.2023063 = 4070402756

Mình nghĩ bạn chép sai phần A của câu hỏi rồi vì mỗi số hạng đều chia hết cho 3 nên xin phép sửa nhé!

\(A=3+6+9+...+2022\)

Số số hạng của biểu thức A là:

\(\left(2022-3\right):3+1=674\) (số)

\(\Rightarrow A=\left(2022+3\right)\cdot674:2\)

\(\Rightarrow A=682425\)

Vậy \(\Rightarrow A=682425\)

\(H=2012\cdot3+2012\cdot4+...+2012\cdot2011\)

\(\Rightarrow H=2012\cdot\left(3+4+...+2011\right)\)

Đặt \(B=3+4+...+2011\)

Số số hạng của biểu thức B là:

\(\left(2011-3\right):1+1=2009\) (số)

\(\Rightarrow B=\left(2011+3\right)\cdot2009:2\)

\(\Rightarrow B=2023063\)

Thay \(B=2023063\) vào H được:

\(H=2012\cdot2023063\)

\(\Rightarrow H=4070402756\)

Vậy \(H=4070402756\)

\(A=3+6+9+...+2023\)

\(A=\left(2023-6\right)\div3+1=\dfrac{2020}{3}\rightarrow\) Đề sai.

\(B=2012.3+2012.4+...+2012.2011\)

\(B=2012.\left(3+4+...+2011\right)\)

Số số hạng:\(\left(2011-3\right)\div1+1=2009\) (số hạng)

Tổng : \(\left(2011+3\right).2009:2=2023063\)

Thay vào B , ta có:

\(B=2012.2023063=470402756\)

1: BC=BH+CH=4+9=13(cm)

Xét ΔHAB vuông tại H và ΔACB vuông tại A có

\(\widehat{HBA}\) chung

Do đó: ΔHAB~ΔACB

=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)

=>\(BA^2=BH\cdot BC=4\cdot13=52\)

=>\(BA=\sqrt{52}=2\sqrt{13}\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AC^2=13^2-\left(2\sqrt{13}\right)^2=117\)

=>\(AC=\sqrt{117}=3\sqrt{13}\left(cm\right)\)

2: ΔHAB~ΔACB

=>\(\dfrac{HA}{AC}=\dfrac{AB}{CB}\)

=>\(HA=\dfrac{AB\cdot AC}{BC}=\dfrac{2\sqrt{13}\cdot3\sqrt{13}}{13}=6\left(cm\right)\)

Xét tứ giác AKHE có \(\widehat{AKH}=\widehat{AEH}=\widehat{KAE}=90^0\)

nên AKHE là hình chữ nhật

=>AH=KE

=>KE=6(cm)

3: Xét ΔAKH vuông tại K và ΔAHB vuông tại H có

\(\widehat{HAB}\) chung

Do đó: ΔAKH~ΔAHB

=>\(\dfrac{AK}{AH}=\dfrac{AH}{AB}\)

=>\(AH^2=AK\cdot AB\left(1\right)\)

Xét ΔAEH vuông tại E và ΔAHC vuông tại H có

\(\widehat{EAH}\) chung

Do đó: ΔAEH~ΔAHC

=>\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\)

=>\(AH^2=AE\cdot AC\left(2\right)\)

Từ (1),(2) suy ra \(AK\cdot AB=AE\cdot AC\)

=>\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)

Xét ΔAKE vuông tại A và ΔACB vuông tại A có

\(\dfrac{AK}{AC}=\dfrac{AE}{AB}\)

Do đó: ΔAKE~ΔACB

4: ta có: ΔABC vuông tại A

mà AI là đường trung tuyến

nên IA=IC

=>ΔIAC cân tại I

=>\(\widehat{IAC}=\widehat{ICA}\)

ΔAKE~ΔACB

=>\(\widehat{AEK}=\widehat{ABC}\)

Ta có: \(\widehat{AEK}+\widehat{IAC}=\widehat{ABC}+\widehat{ACB}=90^0\)

=>EK\(\perp\)AI tại N

1. Tính AB, AC:

• Áp dụng định lý Pitago trong tam giác vuông AHB:
  • AB² = AH² + HB²
  • AH² = AB² - HB²
• Áp dụng định lý Pitago trong tam giác vuông AHC:
  • AC² = AH² + HC²
  • AH² = AC² - HC²
• Từ hai phương trình trên, ta có: AB² - HB² = AC² - HC²
• Suy ra: AB² = AC² - HC² + HB²
• Thay số: AB² = AC² - 9² + 4² = AC² - 65
• Áp dụng định lý Pitago trong tam giác vuông ABC:
  • BC² = AB² + AC²
  • BC² = (AC² - 65) + AC² = 2AC² - 65
• Thay BC = HB + HC = 4 + 9 = 13
  • 13² = 2AC² - 65
  • 2AC² = 13² + 65 = 224
  • AC² = 112
  • AC = √112 = 4√7 cm
• Thay AC vào phương trình AB² = AC² - 65:
  • AB² = (4√7)² - 65 = 112 - 65 = 47
  • AB = √47 cm

2. Tính KE:

• Áp dụng định lý Pitago trong tam giác vuông AKE:
  • KE² = AK² + AE²
• Áp dụng định lý Pitago trong tam giác vuông AHB:
  • AK² = AH² - HK²
• Áp dụng định lý Pitago trong tam giác vuông AHC:
  • AE² = AH² - HE²
• Thay vào phương trình KE²:
  • KE² = (AH² - HK²) + (AH² - HE²) = 2AH² - (HK² + HE²)
• Ta có: HK + HE = BC = 13 cm
• Áp dụng định lý Pitago trong tam giác vuông HKE:
  • KE² = HK² + HE² = (HK + HE)² - 2HK.HE = 13² - 2HK.HE
• Suy ra: 2AH² - (HK² + HE²) = 13² - 2HK.HE
• 2AH² = 13² + 2HK.HE
• AH² = (13² + 2HK.HE) / 2
• Thay AH² = AB² - HB²:
  • AB² - HB² = (13² + 2HK.HE) / 2
  • 2(AB² - HB²) = 13² + 2HK.HE
  • 2HK.HE = 2(AB² - HB²) - 13²
  • HK.HE = (AB² - HB²) - 13²/2
  • HK.HE = (47 - 4²) - 13²/2 = -65/2
• Vì HK và HE đều dương nên HK.HE = -65/2 là vô lý.
• Vậy, không thể tính KE bằng cách này.

3. Chứng minh AB.AK = AE.AC; AKE ~ ACB:

• Chứng minh AB.AK = AE.AC:
  • Xét tam giác vuông AHB và tam giác vuông AHC, ta có:
    • Góc BAH = Góc CAH (cùng bằng 90 độ)
    • Góc ABH = Góc ACH (cùng phụ với góc BAH)
  • Suy ra tam giác AHB đồng dạng với tam giác AHC (g-g)
  • Do đó: AB/AC = AH/AH = 1
  • Suy ra: AB = AC
  • Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
    • Góc KAE = Góc CAB (cùng bằng 90 độ)
    • Góc AKE = Góc ACB (cùng phụ với góc KAE)
  • Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)
  • Do đó: AK/AC = AE/AB
  • Suy ra: AB.AK = AE.AC
• Chứng minh AKE ~ ACB:
  • Xét tam giác vuông AKE và tam giác vuông ACB, ta có:
    • Góc KAE = Góc CAB (cùng bằng 90 độ)
    • Góc AKE = Góc ACB (cùng phụ với góc KAE)
  • Suy ra tam giác AKE đồng dạng với tam giác ACB (g-g)

4. Chứng minh AI vuông góc KE tại N:

• Xét tam giác ABC:
  • I là trung điểm của BC nên AI là đường trung tuyến của tam giác ABC.
• Xét tam giác AKE:
  • N là giao điểm của AI và KE nên N là trọng tâm của tam giác AKE.
• Theo tính chất trọng tâm của tam giác:
  • Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
  • Do đó: AN = 2/3 AI
• Xét tam giác vuông AHI:
  • AI là đường trung tuyến của tam giác vuông AHI nên AI = 1/2 HI.
• Suy ra:
  • AN = 2/3 AI = 2/3 * (1/2 HI) = 1/3 HI
  • Do đó: IN = AI - AN = 1/2 HI - 1/3 HI = 1/6 HI
• Xét tam giác vuông HKE:
  • N là trung điểm của KE nên HN là đường trung tuyến của tam giác vuông HKE.
• Theo tính chất đường trung tuyến của tam giác vuông:
  • Đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
  • Do đó: HN = 1/2 KE
• Suy ra:
  • IN = 1/6 HI = 1/2 HN
  • Do đó: HN = 3IN
• Xét tam giác HIN:
  • HN = 3IN nên tam giác HIN vuông tại I (định lý đảo của định lý Pytago).
• Kết luận:
  • AI vuông góc KE tại N.

Lưu ý:

• Trong bài toán này, không thể tính KE bằng cách sử dụng định lý Pitago trong tam giác vuông HKE vì HK.HE là một số âm.
• Việc chứng minh AB.AK = AE.AC và AKE ~ ACB là cần thiết để chứng minh AI vuông góc KE tại N.
• Việc chứng minh AI vuông góc KE tại N là một ứng dụng của tính chất trọng tâm của tam giác và tính chất đường trung tuyến của tam giác vuông.
•  

a: Xét tứ giác ABMD có

AD//BM

AB//MD

Do đó: ABMD là hình bình hành

=>AD=BM; AB=MD

Xét tứ giác AEMC có

AE//MC

AC//ME

Do đó: AEMC là hình bình hành

=>AE=MC; ME=AC

Ta có: AE+AD=DE
BM+MC=BC

mà AD=BM và MC=AE

nên DE=BC

Xét ΔABC và ΔMDE có

AB=MD

BC\DE

AC=ME

Do đó: ΔABC=ΔMDE

b: Ta có: AEMC là hình bình hành

=>AM cắt EC tại trung điểm của mỗi đường(1)

Ta có: ABMD là hình bình hành

=>AM cắt BD tại trung điểm của mỗi đường(2)

Từ (1),(2) suy ra AM,EC,BD đồng quy

\(x^3+6x^2+11x+6\)

\(=x^3+x^2+5x^2+5x+6x+6\)

\(=x^2\left(x+1\right)+5x\left(x+1\right)+6\left(x+1\right)\)

\(=\left(x+1\right)\left(x^2+5x+6\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\)

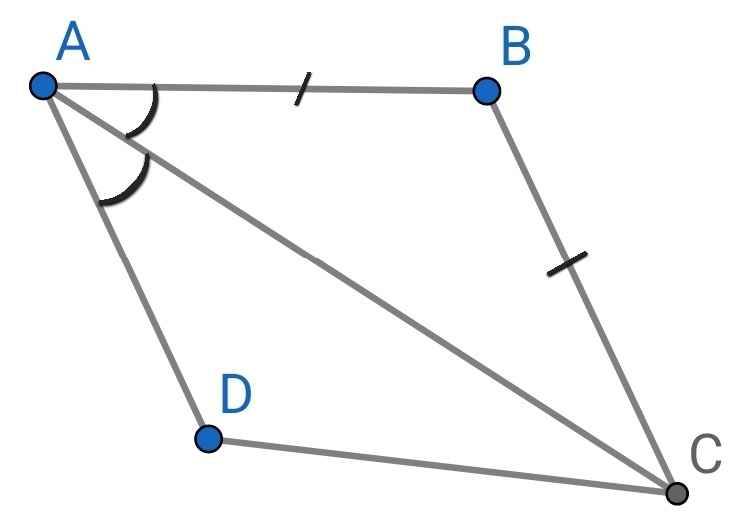
∆ABC có:

AB = BC (gt)

⇒ ∆ABC cân tại B

⇒ ∠BAC = ∠BCA (1)

Do AC là tia phân giác của ∠BAD (gt)

⇒ ∠DAC = ∠BAC (2)

Từ (1) và (2) ⇒ ∠BCA = ∠DAC

Mà ∠BCA và ∠DAC là hai góc so le trong

⇒ BC // AD

⇒ ABCD là hình thang

a) Do x là số nguyên nên 2x + 1 là số nguyên lẻ

Để phân thức đã cho nhận giá trị nguyên thì 2 ⋮ (2x + 1)

⇒ 2x + 1 ∈ Ư(2) = {-1; 1}

⇒ 2x ∈ {-2; 0}

⇒ x ∈ {-1; 0}

Vậy có 2 giá trị nguyên của x thỏa mãn yêu cầu đề bài

b) Ta có:

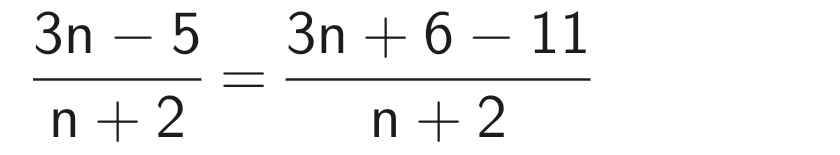
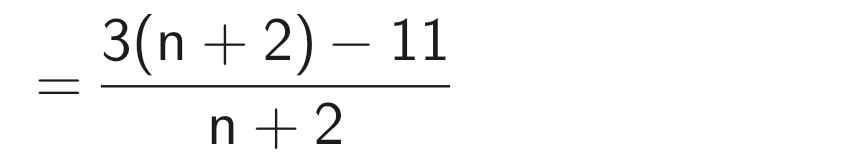
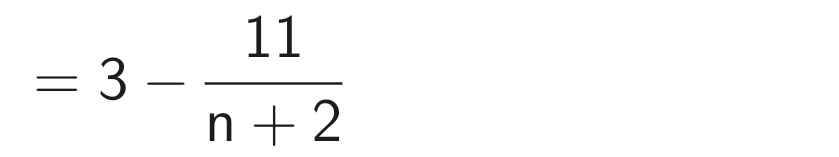
Để phân thức đã cho nhận giá trị nguyên thì 11 ⋮ (n + 2)

⇒ n + 2 ∈ Ư(11) = {-11; -1; 1; 11}

⇒ n ∈ {-13; -3; -1; 9}

Vậy có 4 giá trị nguyên của n thỏa mãn yêu cầu đề bài