 Giúp tớ vs ạ!!! cảm ơn!!!
Giúp tớ vs ạ!!! cảm ơn!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1
a: ĐKXĐ: \(n\ne4\)
Để A nguyên thì \(3n+9⋮n-4\)
=>\(3n-12+21⋮n-4\)
=>\(21⋮n-4\)
=>\(n-4\in\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
=>\(n\in\left\{5;3;7;1;11;-3;25;-17\right\}\)
b: ĐKXĐ: n<>1/2
Để B nguyên thì \(6n+5⋮2n-1\)
=>\(6n-3+8⋮2n-1\)
=>\(8⋮2n-1\)
mà 2n-1 lẻ(do n nguyên)
nên \(2n-1\in\left\{1;-1\right\}\)
=>\(n\in\left\{1;0\right\}\)
Bài 2:
a: \(\left|x-\dfrac{1}{2}\right|>=0\forall x\)
=>\(-\dfrac{1}{2}\left|x-2\right|< =0\forall x\)
=>\(A=-\dfrac{1}{2}\left|x-2\right|+\dfrac{3}{2}< =\dfrac{3}{2}\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
b: \(\left|\dfrac{1}{2}-x\right|>=0\forall x\)
=>\(-2,3\left|\dfrac{1}{2}-x\right|< =0\forall x\)
=>\(D=-2,3\left|\dfrac{1}{2}-x\right|+2< =2\forall x\)
Dấu '=' xảy ra khi 1/2-x=0
=>x=1/2
Bài 1:
\(A=\dfrac{3n+9}{n-4}=\dfrac{3n-12}{n-4}+\dfrac{21}{n-4}=3+\dfrac{21}{n-4}\)
Để A nguyên thì \(\dfrac{21}{n-4}\) phải nguyên hay \(\left(n-4\right)\inƯ\left(21\right)=\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
\(\Rightarrow n\in\left\{5;3;7;1;11;-3;25;-17\right\}\) (thoả mãn điều kiện)
Vậy...
\(B=\dfrac{6n+5}{2n-1}=\dfrac{6n-3}{2n-1}+\dfrac{8}{2n-1}=3+\dfrac{8}{2n-1}\)
Để B nguyên thì \(\dfrac{8}{2n-1}\) phải nguyên hay \(\left(2n-1\right)\inƯ\left(8\right)=\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
Mặt khác: Vì n nguyên nên 2n-1 là số lẻ
Do đó: \(\left(2n-1\right)\in\left\{1;-1\right\}\)
\(\Rightarrow n\in\left\{1;0\right\}\)
Vậy....

\(12\cdot53+53\cdot47-53\cdot41\)
\(=53\cdot\left(12+47-41\right)\)
\(=53\cdot18=954\)

a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
b: A nằm giữa O và B
=>OA+AB=OB
=>AB+3=6
=>AB=3(cm)
c: Vì A nằm giữa O và B
nên AO và AB là hai tia đối nhau
=>AO và Ax là hai tia đối nhau
Trên tia AO, ta có: AO<AM
nên O nằm giữa A và M
=>AO+OM=AM
=>OM+3=6
=>OM=3(cm)
=>OM=OA(=3cm)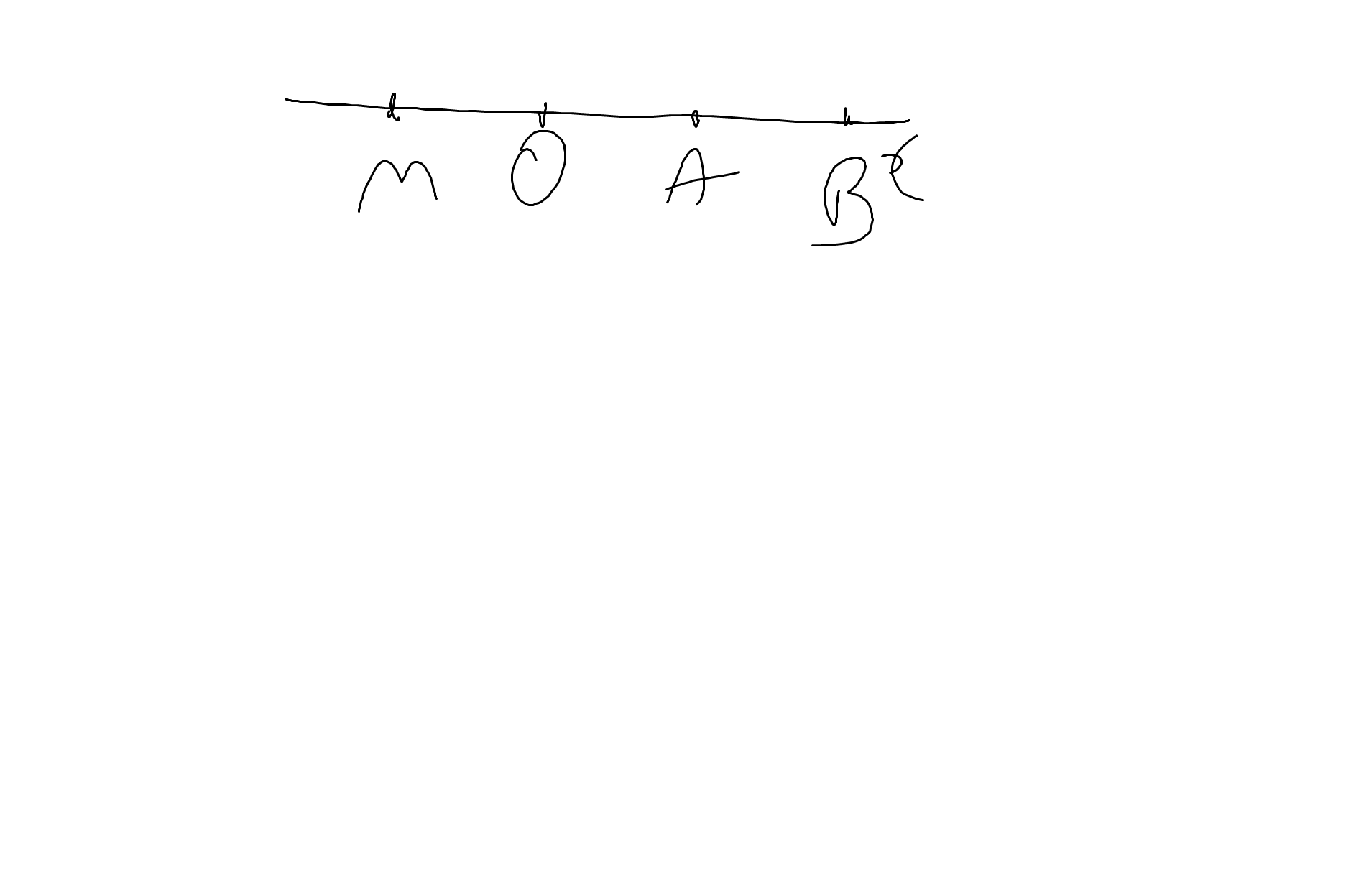

1. B C D
2. G H I
3. J K L
4. C D E
5. L M N
6. O P Q
7. R S T
8. T U V
9. V W X
10. D E F
11. F G H
12. N O P

Vì nếu tăng chiều rộng thêm 20m thì hình chữ nhật trở thành hình vuông nên chiều dài hơn chiều rộng 20m.
Coi chiều dài là 3 phần, chiều rộng là 2 phần, khi đó hiệu số phần bằng nhau là:
$3-2=1$ (phần)
Chiều dài hình chữ nhật là:
$20:1\times3=60(m)$
Chiều rộng hình chữ nhật là:
$60-20=40(m)$
Diện tích hình chữ nhật là:
$60\times40=2400(m^2)$

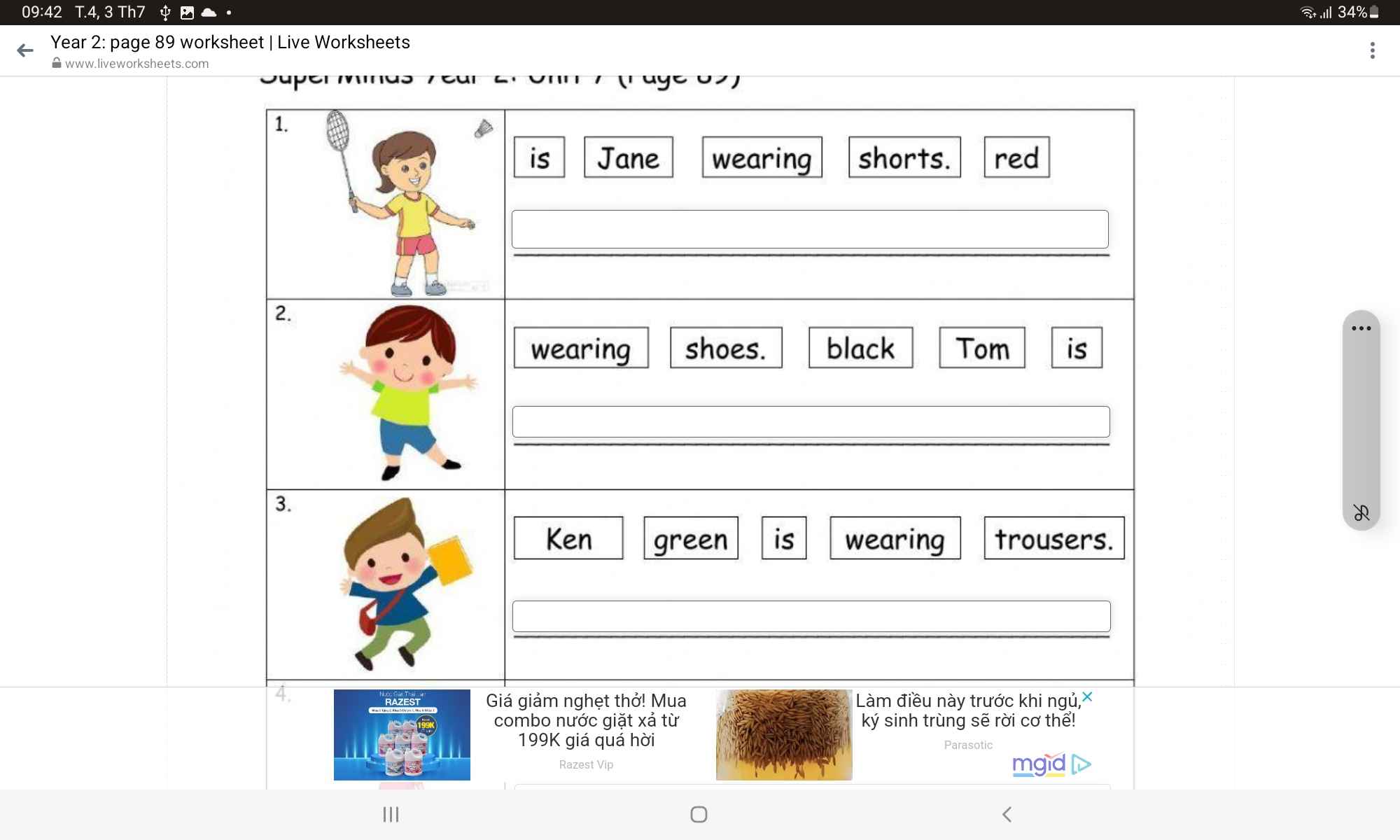
1. Jane is wearing red shorts.
2. Tom is wearing black shoes.
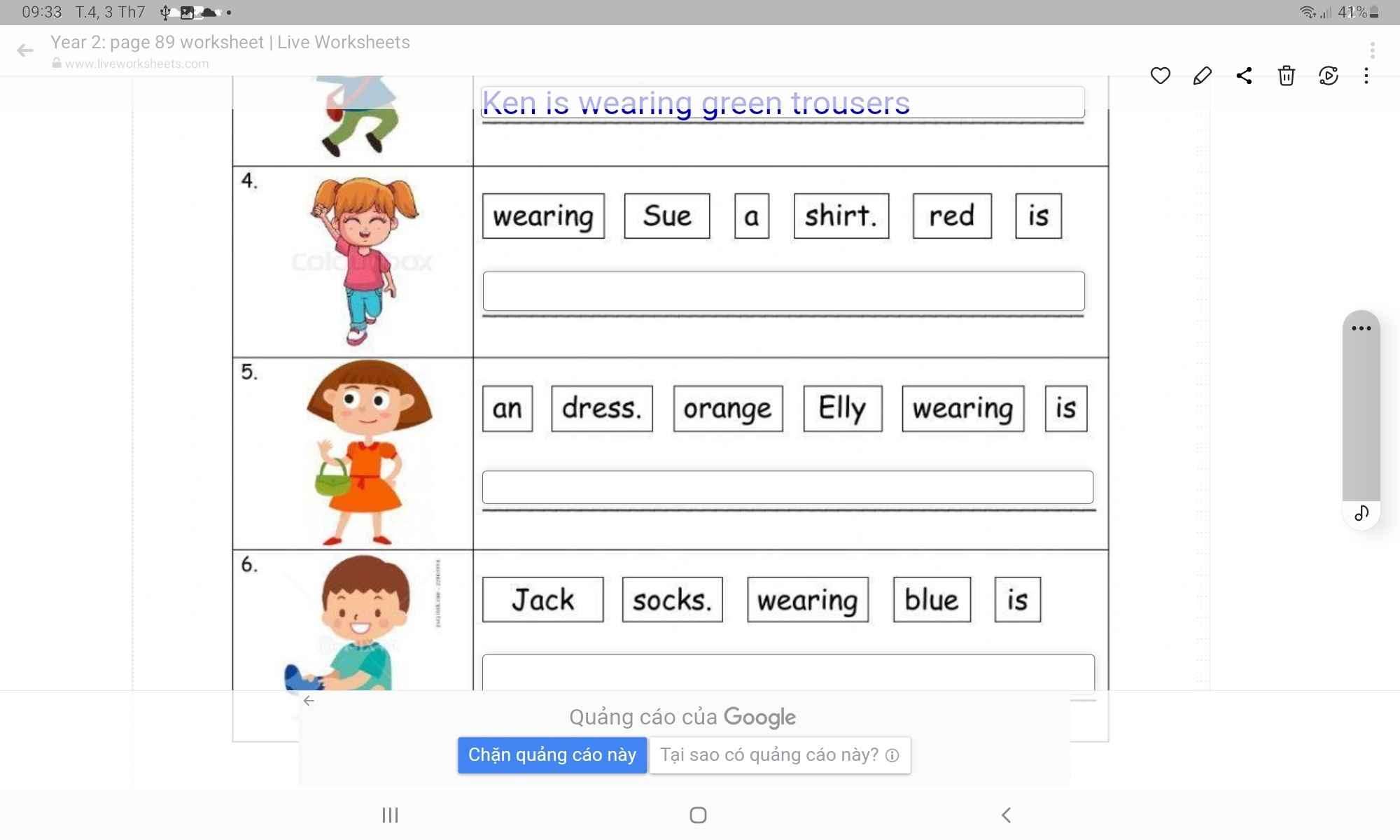
3. Ken is wearing green trousers.
4. Sue is wearing a red shirt.
5. Elly is wearing an orange dress.
6. Jack is wearing blue socks.

|3x+4|=x+2
=>\(\left\{{}\begin{matrix}x+2>=0\\\left(3x+4\right)^2=\left(x+2\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-2\\\left(3x+4-x-2\right)\left(3x+4+x+2\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-2\\\left(2x+2\right)\left(4x+6\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-2\\x\in\left\{-1;-\dfrac{3}{2}\right\}\end{matrix}\right.\Leftrightarrow x\in\left\{-1;-\dfrac{3}{2}\right\}\)
|5x-6|=4-x
=>\(\left\{{}\begin{matrix}4-x>=0\\\left(5x-6\right)^2=\left(4-x\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =4\\\left(5x-6-4+x\right)\left(5x-6+4-x\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =4\\\left(6x-10\right)\left(4x-2\right)=0\end{matrix}\right.\Leftrightarrow x\in\left\{\dfrac{5}{3};\dfrac{1}{2}\right\}\)
|5-2x|=x-3
=>|2x-5|=x-3
=>\(\left\{{}\begin{matrix}x-3>=0\\\left(2x-5\right)^2=\left(x-3\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=3\\\left(2x-5\right)^2-\left(x-3\right)^2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=3\\\left(2x-5-x+3\right)\left(2x-5+x-3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=3\\\left(x-2\right)\left(3x-8\right)=0\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
|3-2x|=6+4x
=>|2x-3|=4x+6
=>\(\left\{{}\begin{matrix}4x+6>=0\\\left(4x+6\right)^2=\left(2x-3\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-\dfrac{3}{2}\\\left(4x+6-2x+3\right)\left(4x+6+2x-3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-\dfrac{3}{2}\\\left(2x+9\right)\left(6x+3\right)=0\end{matrix}\right.\Leftrightarrow x=-\dfrac{1}{2}\)
|6-3x|=3x
=>|3x-6|=3x
=>|x-2|=x
=>\(\left\{{}\begin{matrix}x>=0\\\left(x-2\right)^2=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=0\\-4x+4=0\end{matrix}\right.\Leftrightarrow x=1\)

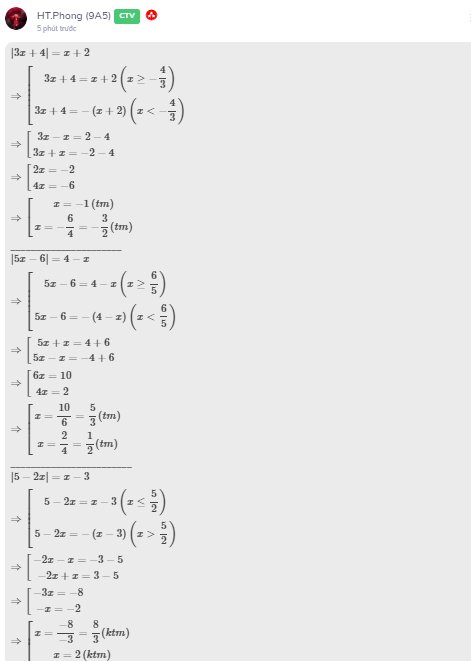
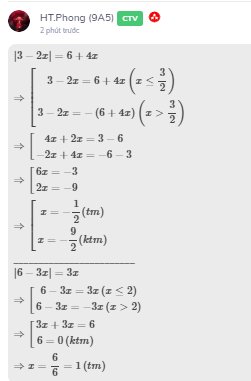
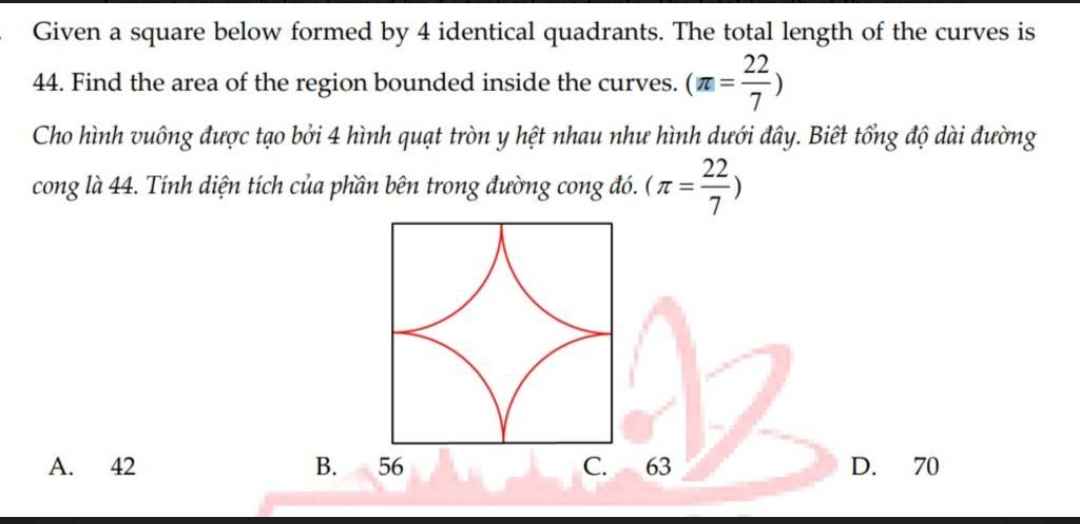
Độ dài 1 đường cong là:
$44:4=11$ (đvi độ dài)
Chu vi bốn hình quạt tròn là:
$11\times4=44$ (đvi độ dài)
Từ bốn hình quạt tròn đó ta ghép được 1 hình tròn. Khi đó:
Độ dài cạnh hình vuông là:
$44:\frac{22}{7}=14$ (đvi độ dài)
Diện tích hình vuông là:
$14\times14=196$ (đvi diện tích)
Diện tích bốn hình quạt tròn là:
$\frac{14}{2}\times\frac{14}{2}\times\frac{22}{7}=154$ (đvi diện tích)
Diện tích của phần bên trong đường cong là:
$196-154=42$ (đvi diện tích)
4 curves form 1 circle
The radius of the circle is:
7.2 = 14
The area of the square is:
14.14 = 196
The area of the region bounded inside the curves is:
196 - 154 = 42