Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A\left(x\right)=3x^2\left(4x^3-2x+\dfrac{1}{3}\right)\\ =3x^2\cdot4x^3-3x^2\cdot2x+3x^2\cdot\dfrac{1}{3}\\ =12x^5-6x^3+x^2\\ B\left(x\right)=4x^3-\dfrac{1}{5}x\left(2x^2-x+5\right)\\ =4x^3-\dfrac{1}{5}x\cdot2x^2+\dfrac{1}{5}x\cdot x-\dfrac{1}{5}x\cdot5\\ =4x^3-\dfrac{2}{5}x^3+\dfrac{1}{5}x^2-x\\ =\dfrac{18}{5}x^3+\dfrac{1}{2}x^5-x\\ C\left(x\right)=\left(x^2-x+1\right)\left(x+1\right)-x\left(x^2+3\right)-15\\ =x^3+1-x^3-3x-15\\ =\left(x^3-x^3\right)-3x+\left(1-15\right)\\ =-3x-14\\ D\left(x\right)=-15x+5x\left(x^2-7x+3\right)-x^2\left(5x-8\right)+27x^2\\ =-15x+5x^3-35x^2+15x-5x^3+8x^2+27x^2\\ =\left(-15x+15x\right)+\left(5x^3-5x^3\right)+\left(8x^2-35x^2+27x^2\right)\\ =0\)

\(a)17\cdot85+15\cdot17-120\\ =17\cdot\left(85+15\right)-120\\ =17\cdot100-120\\ =1700-120\\ =1580\\ b)5\cdot7^2-24:2^3\\ =5\cdot49-24:8\\ =245-3\\ =242\\ c)3^3\cdot22-27\cdot19\\ =27\cdot22-27\cdot19\\ =27\cdot\left(22-19\right)\\ =27\cdot3\\ =81\\ d)-\left|-13\right|+\left(-23\right)\\ =-13+\left(-23\right)\\ =-36\\ e)-\left|-13\right|+\left|-25\right|+\left|12\right|\\ =-13+25+12\\ =12+12\\ =24\\ f)23-\left(12-4^2\right)+\left|15\right|\\ =23-\left(12-16\right)+15\\ =23-\left(-4\right)+15\\ =23+4+15\\ =27+15\\ =42\)

\(a)\dfrac{1}{2}x+199=127\cdot36+36\cdot73-30\cdot40\\\dfrac{ 1}{2}x+199=36\cdot\left(127+73\right)-30\cdot40\\ \dfrac{1}{2}x+199=36\cdot200-1200\\ \dfrac{1}{2}x+199=7200-1200\\ \dfrac{1}{2}x+199=6000\\ \dfrac{1}{2}x=6000-199\\ \dfrac{1}{2}x=5801\\ x=5801:\dfrac{1}{2}=11602\)
\(b)\dfrac{3}{2}:x+\dfrac{1}{3}=\dfrac{19}{21}\cdot\dfrac{25}{3}-\dfrac{16}{21}\cdot\dfrac{25}{3}+\dfrac{1}{7}\\ \dfrac{3}{2}:x+\dfrac{1}{3}=\dfrac{25}{3}\cdot\left(\dfrac{19}{3}-\dfrac{16}{3}\right)+\dfrac{1}{7}\\ \dfrac{3}{2}:x+\dfrac{1}{3}=\dfrac{25}{3}+\dfrac{1}{7}\\ \dfrac{3}{2}:x=\dfrac{25}{3}-\dfrac{1}{3}+\dfrac{1}{7}\\ \dfrac{3}{2}:x=8+\dfrac{1}{7}\\ \dfrac{3}{2}:x=\dfrac{57}{7}\\ x=\dfrac{3}{2}:\dfrac{57}{7}\\ x=\dfrac{21}{114}\)
\(c)\left(x-\dfrac{1}{2025}\right):\dfrac{1}{2}=\dfrac{\dfrac{2023}{3}-\dfrac{2023}{5}-\dfrac{2023}{9}}{\dfrac{2025}{6}-\dfrac{2025}{10}-\dfrac{2025}{18}}\\ \left(x-\dfrac{1}{2025}\right):\dfrac{1}{2}=\dfrac{\dfrac{4046}{6}-\dfrac{4046}{10}-\dfrac{4046}{18}}{2025\left(\dfrac{1}{6}-\dfrac{1}{10}-\dfrac{1}{9}\right)}\\ \left(x-\dfrac{1}{2025}\right):\dfrac{1}{2}=\dfrac{4046\left(\dfrac{1}{6}-\dfrac{1}{10}-\dfrac{1}{9}\right)}{2025\left(\dfrac{1}{6}-\dfrac{1}{10}-\dfrac{1}{9}\right)}\\ \left(x-\dfrac{1}{2025}\right):\dfrac{1}{2}=\dfrac{4046}{2025}\\ x-\dfrac{1}{2025}=\dfrac{4046}{2025}\cdot\dfrac{1}{2}\\ x-\dfrac{1}{2025}=\dfrac{2023}{2025}\\ x=\dfrac{2023}{2025}+\dfrac{1}{2025}\\ x=\dfrac{2024}{2025}\)

\(a)\left[\left(1\dfrac{2}{3}\right)^2\right]^3\\ =\left(1\dfrac{2}{3}\right)^{2\cdot3}\\ =\left(\dfrac{5}{3}\right)^6\\ b)\left(-0,18^3\right)^7\\=\left(-0,18\right)^{3\cdot7}\\ =\left(-0,18\right)^{21}\\ c)\left(\dfrac{1}{3^2}\right)^6\\ =\left[\left(\dfrac{1}{3}\right)^2\right]^6\\ =\left(\dfrac{1}{3}\right)^{2\cdot6}\\ =\left(\dfrac{1}{3}\right)^{12}\)

\(\left|x+\dfrac{1}{1\cdot3}\right|+\left|x+\dfrac{1}{3\cdot5}\right|+...+\left|x+\dfrac{1}{197\cdot199}\right|=100x\)
Số lượng số hạng là: \(\left(199-3\right):2+1=99\) (số hạng)
TH1: \(x\ge-\dfrac{1}{197\cdot199}\)
\(=>\left(x+\dfrac{1}{1\cdot3}\right)+\left(x+\dfrac{1}{3\cdot5}\right)+...+\left(x+\dfrac{1}{197\cdot199}\right)=100x\\ =>\left(x+x+...+x\right)+\left(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{197\cdot199}\right)\\ =>99x+\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{197\cdot199}\right)\\ =>100x-99x=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{197}-\dfrac{1}{199}\right)\\ =>x=\dfrac{1}{2}\cdot\left(1-\dfrac{1}{199}\right)=\dfrac{1}{2}\cdot\dfrac{198}{199}\\ =>x=\dfrac{99}{199}\left(tm\right)\)
TH2: \(x\le-\dfrac{1}{1\cdot3}\)
\(=>-\left(x+\dfrac{1}{1\cdot3}\right)-\left(x+\dfrac{1}{3\cdot5}\right)-...-\left(x+\dfrac{1}{197\cdot199}\right)=100x\\ =>-\left[\left(x+x+...+x\right)+\left(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{197\cdot199}\right)\right]=100x\\ =>-\left[99x+\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{197\cdot199}\right)\right]=100\\ =>-99x-\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{197}-\dfrac{1}{199}\right)=100x\\ =>100x+99x=-\dfrac{1}{2}\left(1-\dfrac{1}{199}\right)\\ =>199x=-\dfrac{1}{2}\cdot\dfrac{198}{199}\\ =>199x=-\dfrac{99}{199}\\ =>x=-\dfrac{99}{199}:199=-\dfrac{99}{39061}\left(ktm\right)\)
Vậy: `x=99/199`

\(\dfrac{4}{\sqrt{5}+\sqrt{3}}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}\right)^2-\left(\sqrt{3}\right)^2}-\sqrt{2^2\cdot5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{5-3}-2\sqrt{5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{2}-2\sqrt{5}\\ =2\left(\sqrt{5}-\sqrt{3}\right)-2\sqrt{5}\\ =2\sqrt{5}-2\sqrt{3}-2\sqrt{5}\\ =-2\sqrt{3}\)

1 We are often taken to the zoo by our father at weekends
2 Hundreds of pupils wre greeted by the smell of fresh paint
3 Noise shouldn't be made by you
4 How can our fields be kept in good condition?
5 Was Lan given an English-Vietnamese dictionary by you?
6 By whom was "Gulliver's travels" written?
7 Why were these books bought?
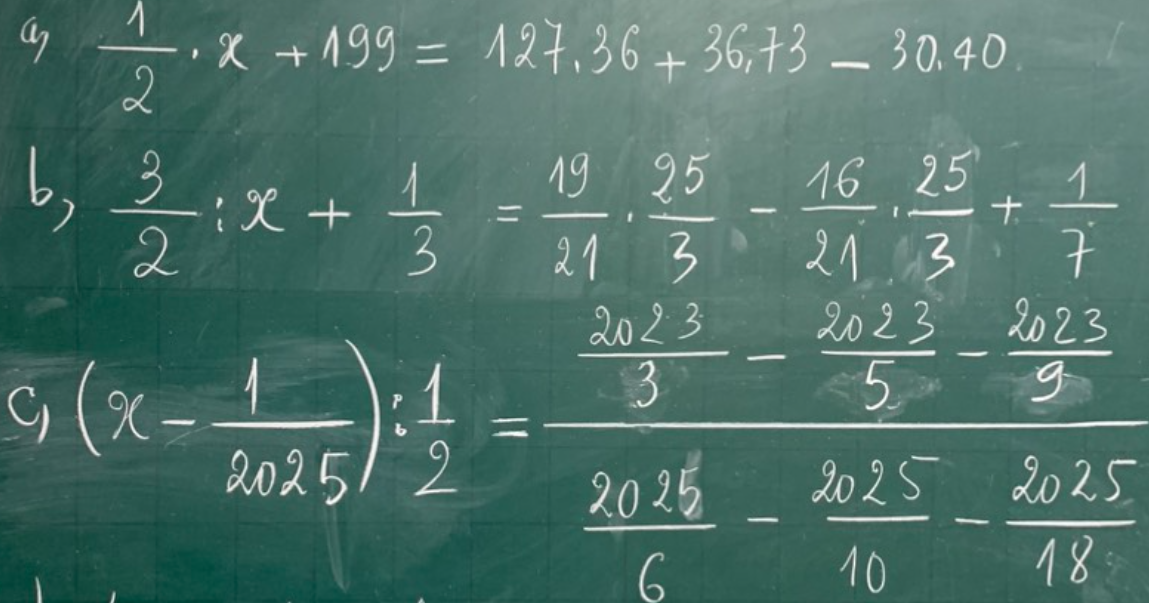
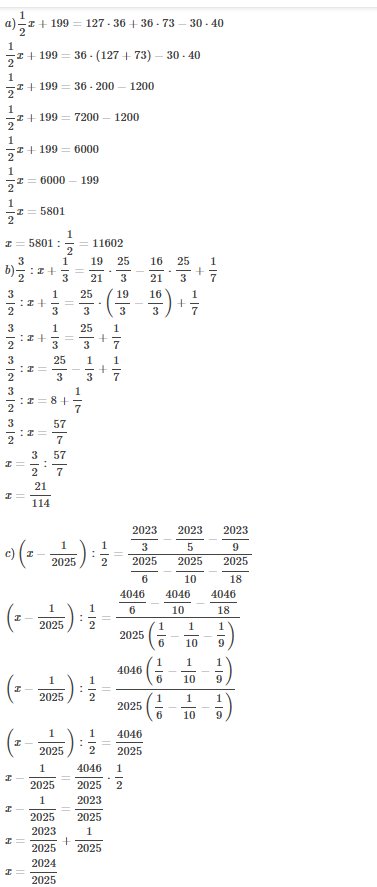
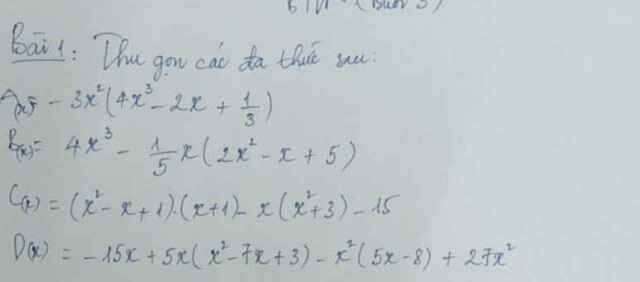

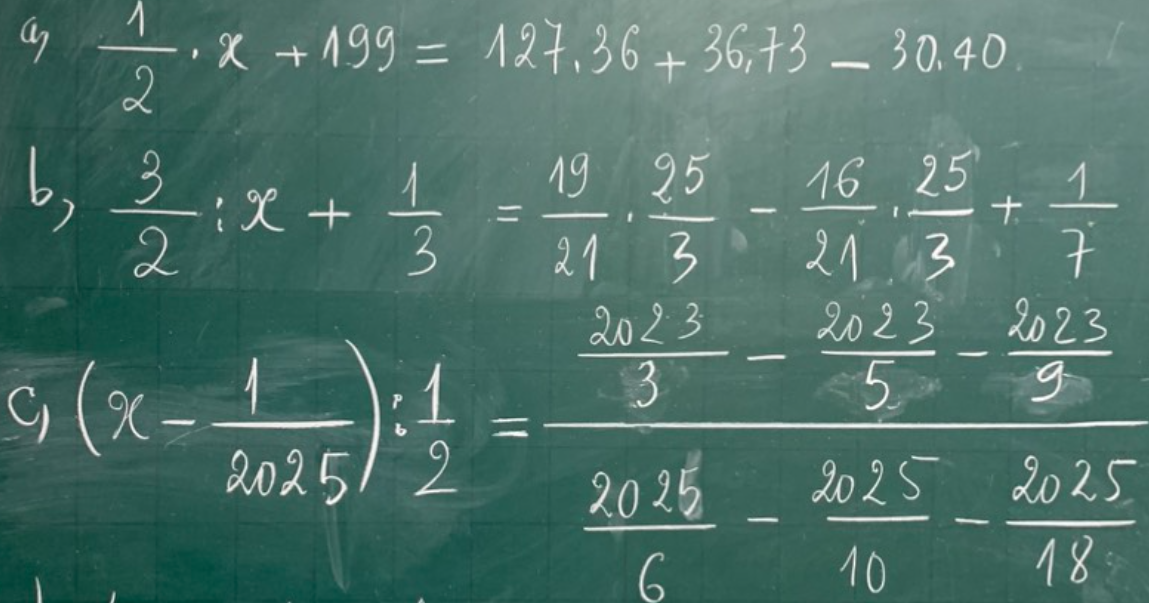
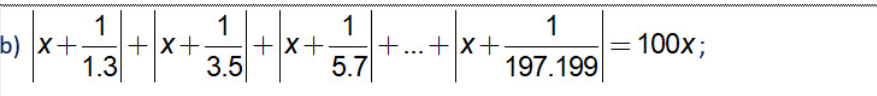
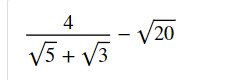
\(a)A\left(x\right)=x^7-3x^2-x^5+x^4-x^2+2x-7\\ =x^7-x^5+x^4-\left(3x^2+x^2\right)+2x-7\\ =x^7-x^5+x^4-4x^2+2x-7\\ B\left(x\right)=x-2x^2+x^4-x^5-x^7-4x^2-1\\ =-x^7-x^5+x^4-\left(2x^2+4x^2\right)+x-1\\ =-x^7-x^5+x^4-6x^2+x-1\)
\(b)A\left(x\right)+B\left(x\right)\\ =\left(x^7-x^5+x^4-4x^2+2x-7\right)+\left(-x^7-x^5+x^4-6x^2+x-1\right)\\ =\left(x^7-x^7\right)-\left(x^5+x^5\right)+\left(x^4+x^4\right)-\left(4x^2+6x^2\right)+\left(2x+x\right)-\left(7+1\right)\\ =-x^5+2x^4-10x^2+3x-8\)
\(A\left(x\right)-B\left(x\right)=\left(x^7-x^5+x^4-4x^2+2x-7\right)-\left(-x^7-x^5+x^4-6x^2+x-1\right)\\ =\left(x^7+x^7\right)+\left(x^5-x^5\right)+\left(x^4-x^4\right)-\left(4x^2-6x^2\right)+\left(2x-x\right)-\left(7-1\right)\\ =2x^7+2x^2+x-6\)
c) Thay x = -1 vào C(x) = A(x) + B(x) ta có:
\(C\left(x\right)=-\left(-1\right)^5+2\cdot\left(-1\right)^4-10\cdot\left(-1\right)^2+3\cdot\left(-1\right)-8\\ =-\left(-1\right)+2\cdot1-10\cdot1-3\cdot1-8\\ =1+2-10-3-8\\ =-18\)