?

\(n_{CO_2}=\dfrac{17,92}{22,4}=0,8\left(mol\right)\)

PT: \(C+O_2\underrightarrow{t^o}CO_2\)

Theo PT: \(n_C=n_{CO_2}=0,8\left(mol\right)\)

\(\Rightarrow m_C=0,8.12=9,6\left(g\right)\)

Độ tinh khiết của mẫu C là: \(\dfrac{9,6}{15}.100\%=64\%\)

program TongCacSoChiaHetChoBa;

var

     n, i, sum: integer;

begin

repeat

          Write('Nhap so nguyen n (3 <= n <= 50): ');

          Readln(n);

     until (n >= 3) and (n <= 50);

     sum := 0;

     for i := 3 to n do

     begin

          if i mod 3 = 0 then

          sum := sum + i;

     end;

     WriteLn('Tong cac so chia het cho 3 trong khoang tu 3 den ', n, ': ', sum);

     ReadLn;

end.

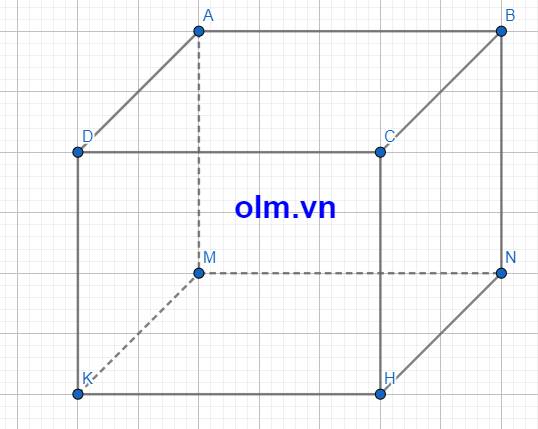
Vì diện tích mặt bên gắn với chiều rộng là 12 cm² nên diện tích mặt bên đó bằng chiều rộng nhân với chiều cao.

Từ lập luận trên ta có:

Chiều rộng của hình hộp chữ nhật là: 

12 : 4 = 3 (cm)

Thể tích của hình hộp chữ nhật là:

5 \(\times\) 3 \(\times\) 4 = 60 (cm³)

Diện tích xung quanh của hình hộp chữ nhật là:

( 5 + 3) \(\times\) 2 \(\times\) 4 = 64 (cm²)

Diện tích hai mặt đáy của hình hộp chữ nhật là:

5 \(\times\) 3 \(\times\) 2 = 30 (cm²)

Diện tích toàn phần của hình hộp chữ nhật là:

64 + 30 = 94 (cm²)

Kết luận: Thể tích hình hộp chữ nhật 60 cm³

               Diện tích toàn phần của hình hộp chữ nhật là: 94 cm²

0,33

- Dễ dàng nhận thấy \(x=-1\) không phải là 1 nghiệm của đa thức P(x).

- Gọi b là 1 nghiệm của đa thức \(P\left(x\right)=x^3+3x^2-1\)

Do đó: \(b^3+3b^2-1=0\)

\(\Rightarrow\left(b^3+3b^2+3b+1\right)-3\left(b+1\right)+1=0\)

\(\Rightarrow\left(b+1\right)^3-3\left(b+1\right)+1=0\)

\(\Rightarrow\dfrac{\left(b+1\right)^3-3\left(b+1\right)+1}{\left(b+1\right)^3}=0\)

\(\Rightarrow\left(\dfrac{1}{b+1}\right)^3-3.\left(\dfrac{1}{b+1}\right)^2+1=0\)

\(\Rightarrow\left(-\dfrac{1}{b+1}\right)^3+3.\left(-\dfrac{1}{b+1}\right)^2-1=0\)

Thay \(x=-\dfrac{1}{b+1}\) vào \(P\left(x\right)=x^3+3x^2-1\) ta được:

\(P\left(-\dfrac{1}{b+1}\right)=\left(-\dfrac{1}{b+1}\right)^3+3.\left(-\dfrac{1}{b+1}\right)^2-1=0\)

\(\Rightarrow-\dfrac{1}{b+1}\) là một nghiệm của đa thức P(x).

Đặt \(a=-\dfrac{1}{b+1}\Rightarrow ab+a+1=0\) \(\Rightarrowđpcm\)