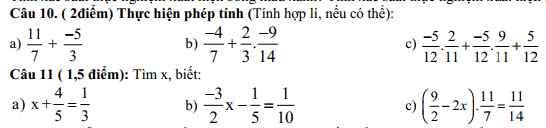
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: Tổng \(3\) số là \(106\) nên chứng tỏ ít nhất một trong \(3\) số đó là số chẵn . Vì \(3\) số là số nguyên tố và chỉ có một số nguyên tố chẵn là \(2\).
\(\Rightarrow\) Số nguyên tố thứ nhất cần tìm là 2.
Tổng \(2\) số nguyên tố còn lại là: \(106-2=104\)
Ta thấy, số nguyên tố lớn nhất và bé hơn \(104\) là \(101\)
\(\Rightarrow\) Số nguyên tố thứ hai là: \(104-101=3\) (thỏa mãn là số nguyên tố)
Vậy: \(3\) số nguyên tố cần tìm là \(2,3,101\)
Từ đó, số nguyên tố lớn nhất thỏa mãn là 101.

Lời giải:
$A=\frac{3}{5}\left(\frac{5}{9.14}+\frac{5}{14.19}+\frac{5}{19.24}+...+\frac{5}{(5n-1)(5n+4)}\right)$
$\frac{3}{5}\left(\frac{14-9}{9.14}+\frac{19-14}{14.19}+\frac{24-19}{19.24}+...+\frac{(5n+4)-(5n-1)}{(5n-1)(5n+4)}\right)$
$=\frac{3}{5}\left(\frac{1}{9}-\frac{1}{14}+\frac{1}{14}-\frac{1}{19}+\frac{1}{19}-\frac{1}{24}+...+\frac{1}{5n-1}-\frac{1}{5n+4}\right)$
$=\frac{3}{5}(\frac{1}{9}-\frac{1}{5n+4})$
$=\frac{1}{15}-\frac{3}{5(5n+4)}< \frac{1}{15}$

Lời giải:
Điều kiện: $x\neq -1$
Ta có: $D=\frac{x^2-1}{x+1}=\frac{(x+1)(x-1)}{x+1}=x-1$
Với mọi $x\in\mathbb{Z}, x\neq -1$ thì $D=x-1$ luôn là số nguyên.
\(D=\dfrac{x^2-1}{x+1}\)
\(D=\dfrac{x^2+x-x-1}{x+1}\)
\(D=\dfrac{x\left(x+1\right)-\left(x+1\right)}{x+1}\)
\(D=\dfrac{\left(x+1\right)\left(x-1\right)}{x+1}\)
\(D=x-1\)
Vậy \(D\in Z\forall x\)

Với $n=1$ thì $3^{2n+1}+2^{2n+2}=3^3+2^4=43$ không chia hết cho 7 bạn nhé. Bạn xem lại.

2020.(20222022 - 11) - 2022.(2020 - 11)
= 2020.20222022 - 2020.11 - 2022.2020.2020 + 2022.11
= 2020. 2022.10001 - 2020.11 - 2022.2020.10001 + 2022.11
= (2020.2022.1001 - 2022.2020.10001) - 11.(2020 -2022)
= 0 - 11.(-2)
= 22

S = 155\(\times\)\(\overline{710y4z16}\)\(⋮\) 33
Vì 155 không chia hết cho 33 nên S ⋮ 33 ⇔ \(\overline{710x4y16}\) ⋮ 33
33 = 3.11 Vì (3; 11) = 1
Nên \(\overline{710x4y16}\) ⋮ 33 ⇔ \(\overline{710x4y16}\) ⋮ 3; 11
⇒ \(\left\{{}\begin{matrix}7+0+4+1=1+x+y+6\\7+1+0+x+4+y+1+1⋮3\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x+y=5\\19+x+y⋮3\end{matrix}\right.\)
⇒ \(x+y\) = 5
Lập bảng ta có:
| \(x+y\) | 5 5 5 5 5 5 |
| \(x\) | 0 1 2 3 4 5 |
| y | 5 4 3 2 1 1 |
Theo bảng trên ta có:
(\(x\);y) = (0;5); (1; 4); (2; 3); (3; 2); (4; 1); (0; 5)

\(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}>\dfrac{a}{a+b+c}+\dfrac{b}{a+b+c}+\dfrac{c}{a+b+c}=1\)
\(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}< \dfrac{a+c}{a+b+c}+\dfrac{b+a}{b+c+a}+\dfrac{c+b}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\)
\(\Rightarrow1< \dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}< 2\)
c; (\(\dfrac{9}{2}\) - 2\(x\)) . \(\dfrac{11}{7}\) = \(\dfrac{11}{14}\)
\(\dfrac{9}{2}\) - 2\(x\) = \(\dfrac{11}{14}\) : \(\dfrac{11}{7}\)
\(\dfrac{9}{2}\) - 2\(x\) = \(\dfrac{1}{2}\)
2\(x\) = \(\dfrac{9}{2}-\dfrac{1}{2}\)
2\(x\) = 4
\(x\) = 4 : 2
\(x\) = 2
Vậy \(x\) = 2
Câu 10 a; \(\dfrac{11}{7}\) + \(\dfrac{-5}{3}\) = \(\dfrac{33}{21}\) + \(\dfrac{-35}{21}\) = \(\dfrac{-2}{21}\)
b; \(\dfrac{-4}{7}\) + \(\dfrac{2}{3}\). \(\dfrac{-9}{14}\) = \(\dfrac{-4}{7}\) + \(\dfrac{-3}{7}\) = -1
c; \(\dfrac{-5}{12}\).\(\dfrac{2}{11}\) + \(\dfrac{-5}{12}\).\(\dfrac{9}{11}\) + \(\dfrac{5}{12}\)
= \(\dfrac{-5}{12}\) x (\(\dfrac{2}{11}\) + \(\dfrac{9}{11}\) - 1)
= - \(\dfrac{5}{12}\) x 0
= 0