có ai lm NY mình ko
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề thi đánh giá năng lực

Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!

\(ℕ,ℤ,ℚ,ℝ,C\) lần lượt là tập hợp các số tự nhiên, số nguyên, số hữu tỉ, số thực và số phức.
Do đó \(ℕ\subsetℤ\subsetℚ\subsetℝ\subset C\)

Gọi số lần giảm giá là x(lần)
(Điều kiện: x∈\(Z^{+}\) )
Giá của mỗi quyển sách sau mỗi lần giảm giá là 15-x(nghìn đồng)
Số quyển sách bán được sau mỗi lần giảm giá là:
200+20x(cuốn)
Số tiền hiệu sách thu được là: \(\left(15-x\right)\left(200+20x\right)\) (nghìn đồng)
Giá vốn của 200+20x cuốn sách là:
\(3\left(200+20x\right)\) (nghìn đồng)
Lợi nhuận của cửa hàng là:
\(T=\left(15-x\right)\left(200+20x\right)-3\left(200+20x\right)=\left(200+20x\right)\left(12-x\right)\)
\(=20\left(x+10\right)\left(12-x\right)=-20\left(x-12\right)\left(x+10\right)\)
\(=-20\left(x^2+10x-12x-120\right)=-20\left(x^2-2x-120\right)\) (nghìn đồng)

Ta có \(\sqrt{2+2\cos2x}=\sqrt{2+2\left(2\cos^2x-1\right)}=\sqrt{4\cos^2x}=2\left|\cos x\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|,\forall x\inℝ\) (1)
Đặt \(g\left(x\right)=f\left(x\right)-\left|\cos x\right|\)
Khi đó (1) \(\Leftrightarrow\left[f\left(x\right)-\left|\cos x\right|\right]+\left[f\left(-x\right)-\left|\cos x\right|\right]=0\)
\(\Leftrightarrow g\left(x\right)+\left[f\left(-x\right)-\left|\cos\left(-x\right)\right|\right]=0\) (do \(\cos x\) là hàm chẵn)
\(\Leftrightarrow g\left(x\right)+g\left(-x\right)=0\)
\(\Leftrightarrow g\left(x\right)=-g\left(-x\right)\)
\(\Leftrightarrow g\left(x\right)\) là hàm lẻ
Khi đó \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ. Thử lại, ta thấy:
(1) \(\Leftrightarrow f\left(x\right)+f\left(-x\right)=g\left(x\right)+\left|\cos x\right|+g\left(-x\right)+\left|\cos\left(-x\right)\right|\)
\(\Leftrightarrow f\left(x\right)+f\left(-x\right)=2\left|\cos x\right|\), thỏa mãn
Vậy \(f\left(x\right)=g\left(x\right)+\left|\cos x\right|\) với \(g\left(x\right)\) là hàm lẻ bất kì có tập xác định là \(ℝ\)
\(\Rightarrow I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}f\left(x\right)dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left[g\left(x\right)+\left|\cos x\right|\right]dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}g\left(x\right)dx+\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\)
\(I=\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|\cos x\right|dx\) (do \(g\left(x\right)\) là hàm lẻ)
\(I=\int\limits^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}\left(-\cos x\right)dx+\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}\cos xdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\left(-\cos x\right)dx\)
\(I=-\sin x|^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}+\sin x|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}-\sin x|^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\)
\(I=6\)

\(x=3y\) và y = 5\(x\) thay y = 5\(x\) vào \(x\) = 3y ta có: \(x\) = 3.5\(x\)
⇒ \(x\) = 15\(x\) ⇒ \(x-15x\) = 0 ⇒ \(-14\)\(x\) = 0 ⇒ \(x=0\)
Thay \(x\) = 0 vào y = 5\(x\) ta được: y= 5.0 = 0
Vậy \(x=3\)y; y = 5\(x\) thì y = 0

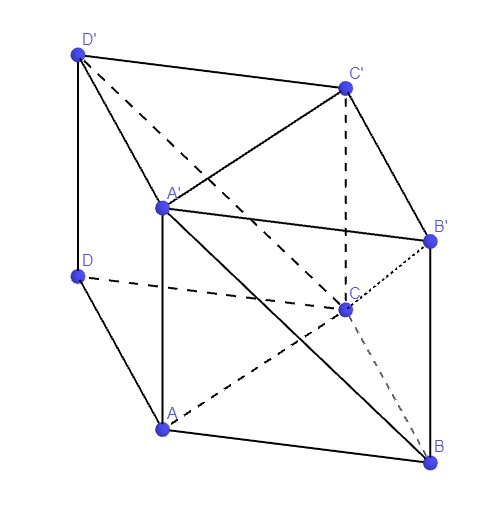
Gọi độ dài cạnh lăng trụ là a
Trong mp (ABC), lấy D đối xứng B qua AC \(\Rightarrow ABCD\) là hình thoi
Trong mp (A'B'C') lấy D' đối xứng B' qua A'C' \(\Rightarrow A'B'C'D'\) là hình thoi
\(\Rightarrow A'BCD'\) là hình bình hành nên \(A'B||D'C\)
\(\Rightarrow\left(A'B,B'C\right)=\left(D'C,B'C\right)=\widehat{B'CD'}\) (nếu nó nhọn, và bằng góc bù với nó nếu nó tù)
\(D'C=A'B=\sqrt{A'A^2+AB^2}=a\sqrt{2}\)
\(B'C=\sqrt{B'B^2+BC^2}=a\sqrt{2}\)
\(B'D'=BD=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
Áp dụng định lý hàm cos:
\(cos\widehat{B'CD'}=\dfrac{B'C^2+D'C^2-B'D'^2}{2B'C.D'C}=\dfrac{1}{4}\)
\(\Rightarrow\left(A'B,B'C\right)\approx75^031'\)

Nếu \(f\left(x\right)=0\) có nghiệm trên \(\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}\left[f\left(x\right)\right]^2=0\) ko thỏa mãn yêu cầu
\(\Rightarrow f\left(x\right)=0\) vô nghiệm trên \(\left[-1;1\right]\)
Khi đó
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)\le0;\forall x\in\left[-1;1\right]\)
Xét hàm \(y=\left[f\left(x\right)\right]^2\) trên \(\left[-1;1\right]\)
\(y=\left[f\left(x\right)\right]^2\Rightarrow y'=2f'\left(x\right).f\left(x\right)\)
Do \(f'\left(x\right)\le0\) và \(f\left(x\right)=0\) vô nghiệm (nên ko đổi dấu) trên \(\left[-1;1\right]\) nên:
TH1: \(f\left(x\right)>0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1>-m\)
\(\Rightarrow-m< \min\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=-1\)
\(\Rightarrow m>1\)
Khi đó \(f'\left(x\right).f\left(x\right)\le0\Rightarrow y=\left[f\left(x\right)\right]^2\) nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(1\right)=\left(1-3+m+1\right)^2=\left(m-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0< 1\left(loại\right)\\m=2\end{matrix}\right.\)
TH2: \(f\left(x\right)< 0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1< -m\)
\(\Rightarrow-m>\max\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=3\)
\(\Rightarrow m< -3\)
Khi đó \(f'\left(x\right).f\left(x\right)\ge0\Rightarrow y=\left[f\left(x\right)\right]^2\) đồng biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(-1\right)=\left(-1+3+m+1\right)^2=\left(m+3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-2>-3\left(loại\right)\\m=-4\end{matrix}\right.\)
Vậy \(m=2;m=-4\) (C đúng)


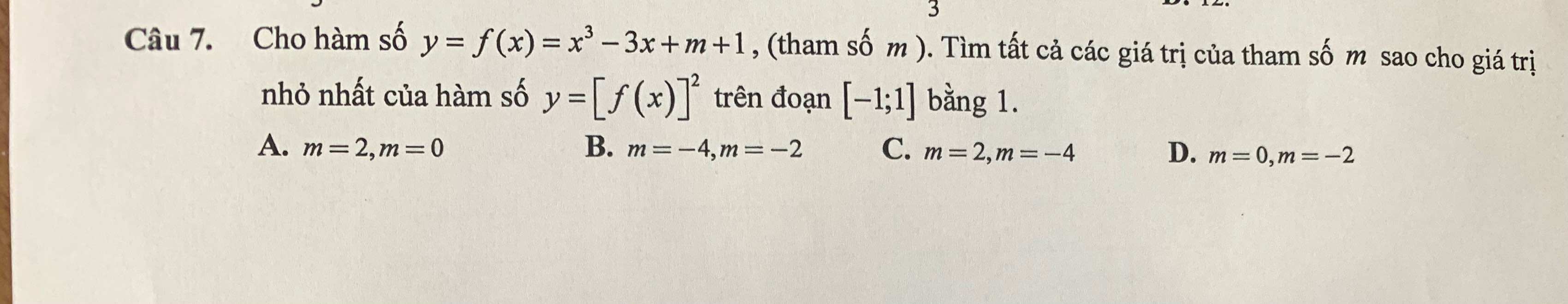
Yêu cầu bạn không đăng linh tinh
ko