KL
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
4.
Đáp án A đúng
\(y'=9x^2+3>0;\forall v\in R\)
6.
Đáp án B đúng
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Do \(\left(2;+\infty\right)\subset\left(1;+\infty\right)\) nên hàm cũng đồng biến trên \(\left(2;+\infty\right)\)
TN
14 tháng 9
Mình nhìn rõ biểu thức trong ảnh là:
$$
V = \sqrt[3]{\,(x^2 - 4)^2\,}.
$$
---
### Phân tích:
* Đây là căn bậc 3 của $(x^2 - 4)^2$.
* Vì căn bậc 3 **luôn xác định với mọi số thực**, nên biểu thức có **tập xác định** là $\mathbb{R}$ (tất cả số thực).
---
### Biến đổi đơn giản hơn:
$$
V = \sqrt[3]{(x^2 - 4)^2} = \big|x^2 - 4\big|^{\tfrac{2}{3}}.
$$
---
✅ Kết luận:
* Tập xác định: $D = \mathbb{R}$.
* Dạng đơn giản: $V = |x^2 - 4|^{2/3}$.
17 tháng 9
ĐKXĐ: \(2x-x^2\ge0\)
=>\(x^2-2x\le0\)
=>x(x-2)<=0
=>0<=x<=2
0<=x<=2 nên 0>=-x>=-2
=>0>=-x+1>=-2+1
=>0>=-x+1>=-1
\(y=\sqrt{2x-x^2}-x\)
=>\(y^{\prime}=\frac{\left(2x-x^2\right)^{\prime}}{2\cdot\sqrt{2x-x^2}}-1=\frac{2-2x}{2\cdot\sqrt{2x-x^2}}-1=\frac{1-x}{\sqrt{2x-x^2}}-1\)
Đặt y'<0
=>\(\frac{1-x}{\sqrt{2x-x^2}}-1<0\) (1)
=>\(\frac{1-x}{\sqrt{2x-x^2}}<1\)
TH1: 1-x<0
=>x>1
=>1<x<=2
Khi đó, ta sẽ có:\(\frac{1-x}{\sqrt{2x-x^2}}<0\) <1
=>(1) luôn đúng với mọi x>1
Kết hợp ĐKXĐ, ta được: 1<x<=2(2)
TH2: 1-x>=0
=>x<=1
(1) sẽ tương đương với: \(\frac{\left(1-x\right)^2}{2x-x^2}<1\)
=>\(\left(1-x\right)^2<2x-x^2\)
=>\(x^2-2x+1-2x+x^2\le0\)
=>\(2x^2-4x+1\le0\)
=>\(x^2-2x+\frac12\le0\)
=>\(x^2-2x+1-\frac12\le0\)
=>\(\left(x-1\right)^2\le\frac12\)
=>\(-\frac{\sqrt2}{2}\le x-1\le\frac{\sqrt2}{2}\)
=>\(\frac{-\sqrt2+2}{2}\le x\le\frac{\sqrt2+2}{2}\)
Kết hợp ĐKXĐ, ta được: \(\frac{-\sqrt2+2}{2}\le x\le\frac{\sqrt2+2}{2}\)
=>0,29<x<1,71(3)
Từ (2),(3) suy ra Hàm số nghịch biến trên khoảng (1;2)
=>Chọn C
17 tháng 9
ĐKXĐ: \(2x-x^2\ge0\)
=>\(x^2-2x\le0\)
=>x(x-2)<=0
=>0<=x<=2
0<=x<=2 nên 0>=-x>=-2
=>0>=-x+1>=-2+1
=>0>=-x+1>=-1
\(y=\sqrt{2x-x^2}-x\)
=>\(y^{\prime}=\frac{\left(2x-x^2\right)^{\prime}}{2\cdot\sqrt{2x-x^2}}-1=\frac{2-2x}{2\cdot\sqrt{2x-x^2}}-1=\frac{1-x}{\sqrt{2x-x^2}}-1\)
Đặt y'<0
=>\(\frac{1-x}{\sqrt{2x-x^2}}-1<0\) (1)
=>\(\frac{1-x}{\sqrt{2x-x^2}}<1\)
TH1: 1-x<0
=>x>1
=>1<x<=2
Khi đó, ta sẽ có:\(\frac{1-x}{\sqrt{2x-x^2}}<0\) <1
=>(1) luôn đúng với mọi x>1
Kết hợp ĐKXĐ, ta được: 1<x<=2(2)
TH2: 1-x>=0
=>x<=1
(1) sẽ tương đương với: \(\frac{\left(1-x\right)^2}{2x-x^2}<1\)
=>\(\left(1-x\right)^2<2x-x^2\)
=>\(x^2-2x+1-2x+x^2\le0\)
=>\(2x^2-4x+1\le0\)
=>\(x^2-2x+\frac12\le0\)
=>\(x^2-2x+1-\frac12\le0\)
=>\(\left(x-1\right)^2\le\frac12\)
=>\(-\frac{\sqrt2}{2}\le x-1\le\frac{\sqrt2}{2}\)
=>\(\frac{-\sqrt2+2}{2}\le x\le\frac{\sqrt2+2}{2}\)
Kết hợp ĐKXĐ, ta được: \(\frac{-\sqrt2+2}{2}\le x\le\frac{\sqrt2+2}{2}\)
=>0,29<x<1,71(3)
Từ (2),(3) suy ra Hàm số nghịch biến trên khoảng (1;2)
=>Chọn C
PD
0
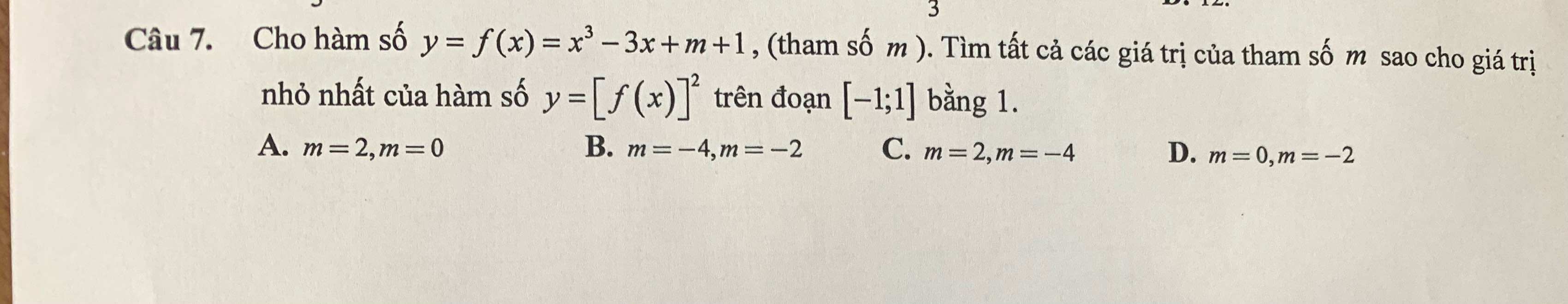
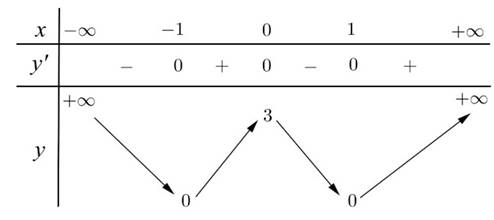
Nếu \(f\left(x\right)=0\) có nghiệm trên \(\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}\left[f\left(x\right)\right]^2=0\) ko thỏa mãn yêu cầu
\(\Rightarrow f\left(x\right)=0\) vô nghiệm trên \(\left[-1;1\right]\)
Khi đó
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)\le0;\forall x\in\left[-1;1\right]\)
Xét hàm \(y=\left[f\left(x\right)\right]^2\) trên \(\left[-1;1\right]\)
\(y=\left[f\left(x\right)\right]^2\Rightarrow y'=2f'\left(x\right).f\left(x\right)\)
Do \(f'\left(x\right)\le0\) và \(f\left(x\right)=0\) vô nghiệm (nên ko đổi dấu) trên \(\left[-1;1\right]\) nên:
TH1: \(f\left(x\right)>0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1>-m\)
\(\Rightarrow-m< \min\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=-1\)
\(\Rightarrow m>1\)
Khi đó \(f'\left(x\right).f\left(x\right)\le0\Rightarrow y=\left[f\left(x\right)\right]^2\) nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(1\right)=\left(1-3+m+1\right)^2=\left(m-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0< 1\left(loại\right)\\m=2\end{matrix}\right.\)
TH2: \(f\left(x\right)< 0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1< -m\)
\(\Rightarrow-m>\max\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=3\)
\(\Rightarrow m< -3\)
Khi đó \(f'\left(x\right).f\left(x\right)\ge0\Rightarrow y=\left[f\left(x\right)\right]^2\) đồng biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(-1\right)=\left(-1+3+m+1\right)^2=\left(m+3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-2>-3\left(loại\right)\\m=-4\end{matrix}\right.\)
Vậy \(m=2;m=-4\) (C đúng)
=5145484985742651291274572147214912742724765142721567