Giúp mình vs ạ. Mik cảm ơn!
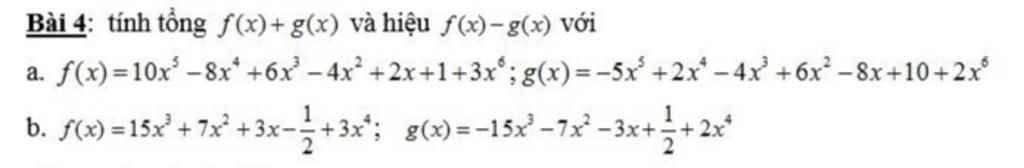
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


chuyển vế sang r phân tích thành nhân tử, có thể dùng máy tính bỏ túi nhé bạn
câu 1: 9\(x^2\) + 12\(x\) + 5 =11
(3\(x\))2 + 2.3.\(x\) .2 + 22 + 1 = 11
(3\(x\) + 2)2 = 11 - 1
(3\(x\) + 2)2 = 10
\(\left[{}\begin{matrix}3x+2=\sqrt{10}\\3x+2=-\sqrt{10}\end{matrix}\right.\)
\(\left[{}\begin{matrix}3x=\sqrt{10}-2\\3x=-\sqrt{10}-2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{\sqrt{10}-2}{3}\\x=\dfrac{-\sqrt{10}-2}{3}\end{matrix}\right.\)
Vậy S = {\(\dfrac{-\sqrt{10}-2}{3}\); \(\dfrac{\sqrt{10}-2}{3}\)}
Câu 2: 6\(x^2\) + 16\(x\) + 12 = 2\(x^2\)
6\(x^2\) + 16\(x\) + 12 - 2\(x^2\) = 0
4\(x^2\) + 16\(x\) + 12 = 0
(2\(x\))2 + 2.2.\(x\).4 + 16 - 4 = 0
(2\(x\) + 4)2 = 4
\(\left[{}\begin{matrix}2x+4=2\\2x+4=-2\end{matrix}\right.\)
\(\left[{}\begin{matrix}2x=-2\\2x=-6\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=-3\end{matrix}\right.\)
S = { -3; -1}
3, 16\(x^2\) + 22\(x\) + 11 = 6\(x\) + 5
16\(x^2\) + 22\(x\) - 6\(x\) + 11 - 5 = 0
16\(x^2\) + 16\(x\) + 6 = 0
(4\(x\))2 + 2.4.\(x\) . 2 + 22 + 2 = 0
(4\(x\) + 2)2 + 2 = 0 (1)
Vì (4\(x\)+ 2)2 ≥ 0 ∀ ⇒ (4\(x\) + 2)2 + 2 > 0 ∀ \(x\) vậy (1) Vô nghiệm
S = \(\varnothing\)
Câu 4. 12\(x^2\) + 20\(x\) + 10 = 3\(x^2\) - 4\(x\)
12\(x^2\) + 20\(x\) + 10 - 3\(x^2\) + 4\(x\) = 0
9\(x^2\) + 24\(x\) + 10 = 0
(3\(x\))2 + 2.3.\(x\).4 + 16 - 6 = 0
(3\(x\) + 4)2 = 6
\(\left[{}\begin{matrix}3x+4=\sqrt{6}\\3x+4=-\sqrt{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}3x=-4+\sqrt{6}\\3x=-4-\sqrt{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{\sqrt{6}-4}{3}\\x=-\dfrac{\sqrt{6}+4}{3}\end{matrix}\right.\)
S = {\(\dfrac{-\sqrt{6}-4}{3}\); \(\dfrac{\sqrt{6}-4}{3}\)}



a)Ta có: BE, CF là pgiac(gt)
=> ∠CBE=∠FEB\(=\dfrac{1}{2}\widehat{ABC}\)
\(\widehat{BCF}=\widehat{ECF}=\dfrac{1}{2}\widehat{ABC}\)
Mà ∠ABC=∠ACB(tam giác ABC cân tại A); ∠BCF=∠CBE(cmt)
Ta có: xét tam giác BFC và tam giác CEB có:
+∠FBC=∠ECB (tam cân)
+BC chung
+∠BCF=∠CBE(cmt)
=> tam giác BFC=tam giác CEB (g.c.g)
=>BF=CE(2 cạnh tương ứng)
Mà AB=AC(gt)
=>AB-BC=AC-CE
=>AF=AE
=>tam giác AFE cân tại A
=> \(\widehat{AFE}=\dfrac{1}{2}\left(180^o-\widehat{A}\right)\)
Mà ∠ABC=1/2(180-A)
=>∠AFE=∠ABC
Mà 2 góc ở vị trí đồng vị
=>EF//BC
=>BFEC là hình thang
Mà ∠CBF=BCE(tam giác cân)
=>BFEC là hình thang cân)
b) Do BFEC là hình thang cân
=>FE//BC; BF=CE(1)
=>góc FEB= góc EBC
Mà BE là pgiac góc B
=>góc FBE=FEB
=> tam giác FBE cân
=>BF=FE (2)
Từ(1);(2)=>BF=FE=EC

vì khi \(a=1\Rightarrow a^4+4a=1^5+4.1=5\) (là số nguyên tố)
\(\Rightarrow m\ne5\Rightarrow a^4+4a\ne5\Rightarrow a\left(a^3+4\right)\ne5\Rightarrow a\ne1\left(a\in Z\right)\)
mà \(\left\{{}\begin{matrix}a^4⋮n\left(a\ne1\Rightarrow n\ne1;n\in Z\right)\\4a⋮4\&a\end{matrix}\right.\)
\(\Rightarrow a^4+4a\) không là số nguyên tố

Để tìm giá trị nhỏ nhất của biểu thức GTNNH=(x-2)(x+1)(x-2)(x+5), ta cần tìm điểm cực tiểu của hàm số.
Đầu tiên, ta tính toán đạo hàm của hàm số GTNNH theo biến x:
GTNNH' = (x+1)(x-2)(x+5) + (x-2)(x+1)(x+5) + (x-2)(x+1)(x-2)
Tiếp theo, ta giải phương trình GTNNH' = 0 để tìm các điểm cực trị của hàm số:
(x+1)(x-2)(x+5) + (x-2)(x+1)(x+5) + (x-2)(x+1)(x-2) = 0
Sau khi giải phương trình trên, ta thu được các giá trị của x là -5, -1 và 2.
Tiếp theo, ta tính giá trị của GTNNH tại các điểm cực trị và so sánh để tìm giá trị nhỏ nhất:
GTNNH(-5) = (-5-2)(-5+1)(-5-2)(-5+5) = 0
GTNNH(-1) = (-1-2)(-1+1)(-1-2)(-1+5) = 0
GTNNH(2) = (2-2)(2+1)(2-2)(2+5) = 0
Như vậy, giá trị nhỏ nhất của biểu thức GTNNH=(x-2)(x+1)(x-2)(x+5) là 0.
\(a,f\left(x\right)+g\left(x\right)\\ =10x^5-5x^5-8x^4+2x^4+6x^3-4x^3-4x^2+6x^2+2x-8x+1+10+3x^6+2x^6\\ =5x^6+5x^5-6x^4+2x^3+2x^2-6x+11\\ f\left(x\right)-g\left(x\right)\\ =3x^6-2x^6+10x^5+5x^5-8x^4-2x^4+6x^3+4x^3-4x^2-6x^2+2x+8x+1-10\\ =x^6+15x^5-10x^4+10x^3-10x^2+10x-9\)
\(b,f\left(x\right) +g \left(x\right)=3x^4+2x^4+15x^3-15x^3+7x^2-7x^2+3x-3x-\dfrac{1}{2}+\dfrac{1}{2}=5x^4\\ f\left(x\right)-g\left(x\right)=3x^4-2x^4+15x^3+15x^3+7x^2+7x^2+3x+3x-\dfrac{1}{2}-\dfrac{1}{2}\\ =x^4+30x^3+14x^2+6x-1\)