Bài 3

a) f(x) = 2x⁶ + 3x² + 5x³ - 2x² + 4x⁴ - x³ + 1 - 4x³ - x⁴

= 2x⁶ + (4x⁴ - x⁴) + (5x³ - x³ - 4x³) + (3x² - 2x²) + 1

= 2x⁶ + 3x⁴ + x² + 1

b) f(1) = 2.1⁶ + 3.1⁴ + 1² + 1

= 2 + 3 + 1 + 1

= 7

f(-1) = 2.(-1)⁶ + 3.(-1)⁴ + (-1)² + 1

= 2 + 3 + 1 + 1

= 7

c) Ta có:

x⁶ ≥ 0 với mọi x ∈ R

⇒ 2x⁶ ≥ 0 với mọi x ∈ R

x⁴ ≥ 0 với mọi x ∈ R

⇒ 3x⁴ ≥ 0 với mọi x ∈ R

x² ≥ 0 với mọi x ∈ R

⇒ 2x⁶ + 3x⁴ + x² + 1 > 0 với mọi x ∈ R

Vậy f(x) không có nghiệm

Bài 4

Cho A(x) = 0

3x - 6 = 0

3x = 6

x = 6 : 3

x = 2

Vậy nghiệm của đa thức A(x) là x = 2

--------

Cho B(x) = 0

(x - 3)(16 - 4x) = 0

x - 3 = 0 hoặc 16 - 4x = 0

*) x - 3 = 0

x = 3

*) 16 - 4x = 0

4x = 16

x = 16 : 4

x = 4

Vậy đa thức B(x) có nghiệm là: x = 3; x = 4

--------

Cho C(x) = 0

x² - 2x = 0

x(x - 2) = 0

x = 0 hoặc x - 2 = 0

*) x - 2 = 0

x = 2

Vậy đa thức C(x) có nghiệm là: x = 0; x = 2

--------

Cho f(x) = 0

5x + 15 = 0

5x = -15

x = -15 : 5

x = -3

Vậy nghiệm của đa thức f(x) là: x = -3

--------

Cho h(x) = 0

x² - 81 = 0

x² = 81

x = -9 hoặc x = 9

Vậy đa thức h(x) có nghiệm là: x = -9; x = 9

--------

g(x) = B(x) nên em xem lại ở câu B(x) nhé

Câu 5:

a: C

b: B

Câu 6: A

Câu 7: D

Câu 8:D

Câu 9: B

Câu 10: A

Câu 11: C

Câu 13: B

Câu 14: D

Câu 15; D

Câu 16; B

Câu 17: C
Câu 18: C

Câu 19: B

Câu 20: B

Không tìm ra được lời giải cho bài này.

a: g=9x

nên g tỉ lệ thuận với x theo hệ số tỉ lệ là k=9

b: s*h=-130

=>s và h tỉ lệ nghịch với nhau theo hệ số tỉ lệ là k=-130

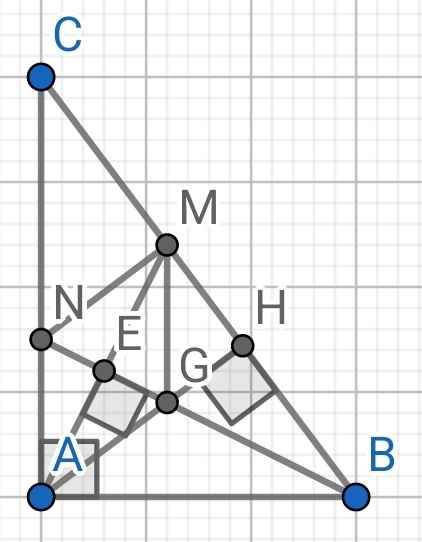
a) Xét hai tam giác vuông: ∆ABE và ∆MBE có:

BA = BM (gt)

BE là cạnh chung

⇒ ∆ABE = ∆MBE (cạnh huyền - cạnh góc vuông)

b) Do ∆ABE = ∆MBE (cmt)

⇒ ∠ABE = ∠MBE (hai góc tương ứng)

⇒ ∠ABN = ∠MBN

Xét ∆ABN và ∆MBN có:

BA = BM (gt)

∠ABN = ∠MBN (cmt)

BN là cạnh chung

⇒ ∆ABN = ∆MBN (c-g-c)

⇒ AN = MN (hai cạnh tương ứng)

c) Do ∆ABN = ∆MBN (cmt)

⇒ ∠BAN = ∠BMN (hai góc tương ứng)

Mà ∠BAN = ∠BAC = 90⁰ (∆ABC vuông tại A)

⇒ ∠BMN = 90⁰

⇒ MN ⊥ BM

⇒ MN ⊥ BC

Lại có AH là đường cao của ∆ABC (gt)

⇒ AH ⊥ BC

Mà MN ⊥ BC (cmt)

⇒ AH // MN

⇒ ∠MGN = ∠ANG (so le trong)

a: ΔABC cân tại A

=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-50^0}{2}=65^0\)

Xét ΔABC có \(\widehat{ACB}>\widehat{BAC}\)

mà AB,BC lần lượt là cạnh đối diện của các góc ACB,BAC

nên AB>BC

b: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

=>\(\widehat{AMB}=\widehat{AMC}\)

mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)

nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)

=>AM\(\perp\)BC

c: ΔAMB=ΔAMC

=>\(\widehat{MAB}=\widehat{MAC}\)

Xét ΔAEM vuông tại E và ΔAFM vuông tại F có

AM chung

\(\widehat{EAM}=\widehat{FAM}\)

Do đó: ΔAEM=ΔAFM

=>AE=AF

Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

nên EF//BC

a) Ta có:

x² ≥ 0 với mọi x ∈ R

⇒ x² + 4 > 0 với mọi x ∈ R

Vậy đa thức đã cho không có nghiệm

b) Ta có:

⇒ (x - 1)² ≥ 0 với mọi x ∈ R

≺ (x - 1)² + 7 > 0 với mọi x ∈ R

Vậy đa thức đã cho không có nghiệm

c) x² + 2x + 2

= x² + x + x + 1 + 1

= (x² + x) + (x + 1) + 1

= x(x + 1) + (x + 1) + 1

= (x + 1)(x + 1) + 1

= (x + 1)² + 1

Ta có:

(x + 1)² ≥ 0 với mọi x ∈ R

⇒ (x + 1)² + 1 > 0 với mọi x ∈ R

Vậy đa thức đã cho không có nghiệm